Свойства определённого интеграла
Перейдем к изучению простейших свойств определенного интеграла.
Свойство линейности. Сумма интегрируемых функций есть интегрируемая функция и произведение интегрируемой функции на число есть также интегрируемая функция. Более того, если 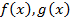 интегрируемы, то для любых чисел
интегрируемы, то для любых чисел 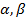 линейная комбинация
линейная комбинация 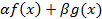 также интегрируема на отрезке
также интегрируема на отрезке 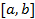 и
и
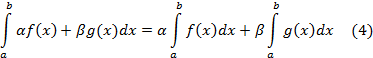
Равенство (4) эквивалентно двум правилам: 1) интеграл от суммы функций равен сумме интегралов и 2) постоянный множитель можно выносить за знак интеграла.
Это свойство следует из соответствующих свойств предела – предел суммы равен сумме пределов и постоянный множитель можно вносить за знак предела.
Изменение ориентации. Равенство 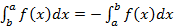 справедливо вне зависимости от расположения точек
справедливо вне зависимости от расположения точек 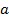 и
и 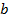 на числовой прямой.
на числовой прямой.
Аддитивность интеграла.Пусть 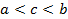 . Тогда функция
. Тогда функция 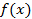 интегрируема на отрезке
интегрируема на отрезке 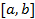 в том и только том случае, когда она интегрируема на
в том и только том случае, когда она интегрируема на 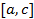 и на
и на 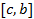 . В этом случае
. В этом случае
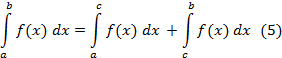
Если точки 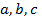 расположены произвольно на числовой прямой и каждый из интегралов в (5) существует, то равенство (5) имеет место.
расположены произвольно на числовой прямой и каждый из интегралов в (5) существует, то равенство (5) имеет место.
Монотонность интеграла. Если 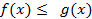 для всех
для всех 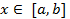 и
и 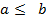 , то
, то
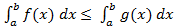 .
.
Дата добавления: 2020-02-05; просмотров: 556;











