Настоящая стоимость и итоговая сумма обыкновенного аннуитета

Настоящая стоимость аннуитета определяется как датированная сумма, эквивалентная всей серии платежей, на начало срока аннуитета. Итоговая сумма аннуитета определяется как датированная сумма, эквивалентная всей серии платежей аннуитета на конец срока. Таким образом, настоящая стоимость обыкновенного аннуитета является эквивалентной суммой, выплачиваемой за один период платежа до даты первой выплаты. Итоговая сумма обыкновенного аннуитета является эквивалентной суммой на момент последнего платежа.

Очевидно, что как настоящая стоимость, так и итоговая сумма аннуитета будет зависеть от нормы процента, используемой в уравнении эквивалентности. Так как период начисления процентов не обязательно совпадает с интервалом платежа, удобно классифицировать аннуитеты с учетом этого. Когда интервал платежа совпадает с периодом начисления процентов, аннуитет называется простым аннуитетом: в противном случае он называется общим аннуитетом. В этом разделе рассматриваются только простые аннуитеты.

Пример 1. Найти текущую стоимость и итоговую сумму обыкновенного аннуитета, состоящего из пяти полугодовых платежей 10000 руб. каждый, если деньги стоят j2 = 4% .

РЕШЕНИЕ Пусть A обозначает настоящую стоимость, а S – итоговую сумму аннуитета. Представим данные на диаграмме

Чтобы определить A выпишем уравнение эквивалентности, используя в качестве даты сравнения начало срока аннуитета. Это даст

A = 10000(1,02) ^-1 + 10000(1,02) ^-2 + 10000(1,02) ^-3 + 10000(1,02) ^-4 + 10000(1,02) ^-5 = 47135 руб.

Подобным образом, для определения S выпишем уравнение эквивалентности, используя в качестве даты сравнения конец срока аннуитета. В этом случае

S = 10000 + 10000(1,02) + 10000(1,02) ² +10000(1,02) ³ + 10000(1,02) ⁴ = 52040 руб.

Способ вычисления A и S , использованный в примере, показывает различие в определениях настоящей стоимости и итоговой суммы, но он является громоздким и неудобным при большом количестве платежей. Более компактный способ расчета можно сформулировать, основываясь на свойствах геометрических прогрессий.

Пусть S будет итоговой суммой обыкновенного простого аннуитета с n платежами по 1 руб. каждый при норме процента iза интервал платежа и пусть A является настоящей стоимостью этого аннуитета. Временная диаграмма платежей аннуитета будет выглядеть следующим образом

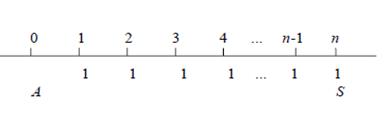
Для нахождения S составим уравнение эквивалентности, используя конец срока как дату сравнения. Тогда получим

S = 1 + 1(1 + i) + 1(1 + i) 2 + ... + 1(1 + i) ^п-1 .

Правая часть равенства является геометрической прогрессией из nчленов, первый член равен 1 и знаменатель прогрессии равен (1 + i).Сумма такой прогрессии равна

S=((1+i)ⁿ-1)/i

Правая часть этого равенства зависит от n и i и имеет общепринятое обозначение s 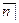_i или s 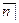при i, читаемое « s уголок n при i»

s 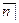_i (или s 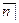при i) =((1+i)ⁿ-1)/i

Если каждая выплата состоит из R руб. , тогда итоговая сумма в R раз больше этой и формула для итоговой суммы S приобретает вид

S=Rs 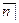_i (4.1)

Для получения настоящей стоимости A этого аннуитета заметим, что A и S являются датированными суммами одной и той же серии платежей и, следовательно, являются эквивалентными суммами. Откуда следует, что

S=A(1 + i) ^п или A = S(1 + i) ^-п(4.2)

Подставляя (4.1) в (4.2), получим

A=R s 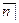_i (1+i)^-n=R(1-(1+i)^-n)/i

Общепринятым обозначением является также следующее

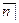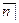a _i=(a при i)= (1-(1+i)^-n)/i

Применение его приводит к следующей формуле для A

A=Ra 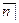_i (4.3)

Равенства (4.1), (4.2) и (4.3) являются основными соотношениями, устанавливающими связь между величинами S , A и R . Два новых обозначения s 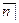_i и a 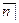_i заменяют всю серию платежей аннуитета одноразовым платежом в соответствующую дату. Они имеют большое распространение в финансовых расчетах, поэтому их величины также табулированы для наиболее часто встречающихся значений параметров n и i .

Пример 2. Иванов будет делать вклады на депозит по 25000 руб. в конце каждого квартала в банк, который установил норму процента 3%, конвертируемую поквартально. Какую сумму он будет иметь в банке через 10 лет, если a) он не имел ничего на банковском счете в начальный

момент; b) он имел на банковском счете 100000 руб. в начальный момент?

РЕШЕНИЕ a) Представим данные на временной диаграмме

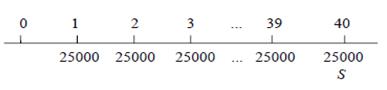
На диаграмме время измеряется интервалами платежа от 0 до 40 и S является суммой на конец сорокового интервала платежа, эквивалентной аннуитету. Так как R = 25000 руб., i= 0,75% за интервал платежа и n= 40, мы имеем

S=R s 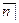_i =25000 s 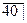_0,0075=25000 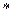46,446481=1161162

b) Дополнительную сумму 100000 руб. следует поместить на временной диаграмме в начальную точку 0. В этом случае уравнение эквивалентности примет вид

S=100000(1,0075)⁴⁰+25000 s₄₀┐_0,0075=134835+1161162=1295997руб.

Пример 3. Петров выплачивает заем, делая платежи по 5000 руб. в конце каждых 6 месяцев. Процентная ставка при получении займа была установлена равной j2 = 5,5% . Какой является неуплаченная часть займа в настоящий момент, если a) осталось сделать 30 платежей, чтобы полностью возместить заем; b) кроме 30 платежей по 5000 руб. необходим еще один взнос 2000 руб. через 6 месяцев?

РЕШЕНИЕ a) Имеющиеся данные представим на диаграмме

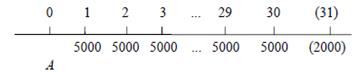
Настоящая стоимость A займа является настоящей стоимостью аннуитета с платежами по 5000 руб., 30 интервалами платежа при норме процента i= 2,75% . Уравнение эквивалентности

A=R a _i =5000₃₀┐₀₀₇₅=5000×20,2459301=101246,51руб.

b) Дополнительная сумма 2000 руб. должна быть помещена на диаграмме в конце 31-го интервала платежа, A равно сумме всех платежей, дисконтированных к началу:

A=5000₃₀┐₀₀₇₅+2000(1,0275)^-31=102109,08руб.