Глава 3 Уравнение эквивалентности

Различные финансовые схемы можно считать эквивалентными в том случае, если они приводят к одному и тому же финансовому результату. В условиях определенности, когда все фигурирующие величины рассматриваются как детерминированные, финансовая эквивалентность сводится к соблюдению требования получить по разным финансовым операциям одинаковые денежные результаты.

С этой целью все платежи по сравниваемым вариантам приводят к одному и тому же моменту в прошлом, будущем или на промежуточную дату. Равенство приведенных величин фактически свидетельствует о безубыточности вносимых изменений для финансовых отношений участников или одного участника, например, инвестора.

Принцип эквивалентности лежит в основе многих финансовых расчетов долгосрочного и кратковременного характера. Он применяется, например, при изменениях условий контрактов: их объединении, досрочном погашении и т. д.

Датированные суммы

Использование значений денежных сумм без указания даты, когда они должны использоваться, является бессмысленным. Очевидно, что 1000 руб. наличными в настоящее время предпочтительнее, чем 1500 руб., которые вы получите через 50 лет. Сумма платежа вместе с датой погашения называется датированной суммой.

В общем случае датированные суммы сравниваются по следующему правилу эквивалентности: сумма Р, полагающаяся на данную дату, эквивалентна при данной норме сложного процента i сумме S , полагающейся нап периодов конверсии позже, если является справедливым хотя бы одно из следующих равенств:

S=P(1+i)ⁿ или P=(1+i)^-n S

Таким образом, накопление или дисконтирование могут рассматриваться как простое преобразование заданной датированной суммы к другой дате. Преобразование делается в соответствии со следующей временной диаграммой:

Прошлая и будущая суммы эквивалентны датированной сумме D.

Важным и полезным свойством эквивалентных датированных сумм является свойство 1: при данной норме сложного процента если А эквивалентно В и В эквивалентно С, то А эквивалентно С.

Для доказательства этого утверждения мы расположим данные на временной диаграмме следующим образом:

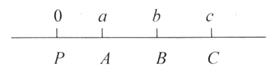
где 0 означает настоящее время и а, b, с представляют числа периодов конверсии от настоящего времени до соответствующих дат погашения.

Если А эквивалентно В, то B=A(1+i)^b-a

Если В эквивалентно С, то C=(1+i)^c-b B

Исключая из этих равенств сумму В, получим, что:

C=A(1+i)^b-a(1+i)^c-b=A(1+i)^c-a

Полученный результат является условием эквивалентности датированных сумм А и С.

Это свойство не имеет места для норм простого процента и норм простого дисконта. Поэтому понятие эквивалентности для этих норм не применяется.