Частотные показатели качества
Частотные показатели качества определяются по частотным характеристи-
кам системы и в частности по амплитудно-частотной характеристике замкнутой
системы и амплитудно-фазо-частотной характеристике разомкнутой системы.
Нормированная амплитудно-частотная характеристика замкнутой системы рис.
4.5 дает следующие показатели качества:
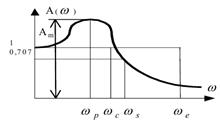
Рис. 4.5
1. Показатель колебательности  ;
;
2. Резонансная частота системы 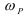 ;
;
3. Частота среза, при которой 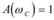
4. Частота пропускания 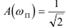 ;
;
5. Эквивалентная частота пропускания ω∋
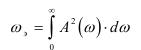
Показатель колебательности М характеризует запас устойчивости системы, чем выше показатель колебательности, тем меньше запас устойчивости. Допустимое значение М выбирается из условия М < 1,1-1,5. Быстродействие системы оценивается по частоте пропускания, чем выше частота пропускания, тем больше быстродействие системы. Использование АФЧХ разомкнутой системы позволяет оценить запас ус-
тойчивости системы на основании запаса устойчивости по амплитуде (модулю) А и фазе ϕ . Эти показатели связаны с критерием устойчивости Найквиста.
Рассмотрим АФЧХ устойчивой системы в окрестностях точки (-1, 0 ) рис .4.6
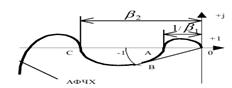
Рис 4.6.
Для общего случая условной устойчивости (рис. 4.6) запас устойчивости
определяется двумя точками а и с по выражениям
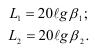
В хорошо демпфированных системах эти величины составляют примерно 6-20 дб, что соответствует 2-10 кратному уменьшению коэффициента усиления системы.
Для абсолютно устойчивых систем L2 →∞ и оценку запаса по модулю производят по L1 Запасом устойчивости по фазе ϕ называется выражение ϕ=180+ψ(ωC) ,
где ψ - аргумент АФЧХ, соответствующий модулю АФЧХ равному 1 (точка b на рис. 4.6). В хорошо демпфированных системах запас по фазе составляет 30 - 600.
Зная частотные характеристики системы можно вычислить их временные характеристики, используя преобразование Фурье.
Можно записать
 где L−1,Φ−1 - обратные преобразования Лапласа и Фурье.
где L−1,Φ−1 - обратные преобразования Лапласа и Фурье.
Переходя к вещественной форме интеграла Фурье, получим
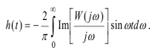
Подставляя сюда W(jω)=U(ω)+ jV(ω), и выделяя мнимую часть, найдем

Для систем невысокого порядка все критерии и показатели качества связаны между собой. Рассмотрим это утверждение на примере колебательного звена с передаточной функцией
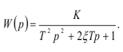
Корни характеристического уравнения найдем из условия
T2 p2 +2ξTp+1=0.
Откуда
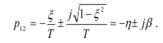
Следовательно, степень устойчивости и степень колебательности для такого звена будут равны
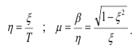
Переходную характеристику звена найдем путем обратного преобразования Лапласа-Карсона от передаточной функции

Максимальные значения вычисляются по следующей формуле:
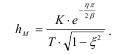
Перерегулирование будет равно:

Время переходного процесса tΠ найдем из условия, при котором  .
.
Амплитудно-частотная характеристика звена будет равна модулю частотной передаточной функции
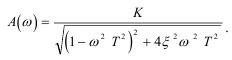
Максимальное значение AM найдем из уравнения 
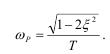
Откуда показатель колебательности М найдем из отношения: 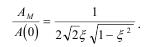
Дата добавления: 2022-07-20; просмотров: 210;











