Корневые показатели качества регулирования

Известно, что характер переходного процесса в системе определяют по ее реакции на единичное ступенчатое воздействие. Переходная характеристика h(t) системы может быть вычислена с помощью обратного преобразования Лапласа (по формулам преобразования Хевисайда):

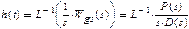(2.8)

Если D(s) не имеет кратных корней, то

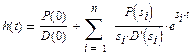, (2.8а)

где s – корни характеристического полинома замкнутой системы D(s)=0.

Из (2.8а) видно, что на характер переходного процесса влияют и числитель и знаменатель П.Ф. замкнутой системы W_gx(s). Если числитель не имеет нулей, т.е. представляет собой постоянную величину, то характер переходных процессов можно оценить по ее полюсам т.е. по корням характеристического уравнения замкнутой системы САУ D(s)=0.

Для приближенной оценки качества переходного процесса в системе нужно на плоскости корней выделить область, в которой располагаются корни ее характеристического уравнения. Чаще всего эту область представляют трапецией (рисунок 2.2). Корни характеристического уравнения располагаются внутри этой трапеции АВСD, на ее сторонах и основаниях хотя бы по одному корню, а вне ее – ни одного.

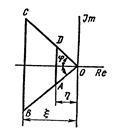
Рисунок 2.2 – Корневые показатели качества

Для выделения этой области на плоскости корней вычисляют параметры: степень устойчивости h, колебательность m и значение x вещественной части максимально удаленного корня от мнимой оси.

Степень устойчивости h - расстояние от мнимой оси до ближайшего корня или ближайшей пары комплексно-сопряженных корней. Степень устойчивости h определяет ближайшее к мнимой оси основание трапеции AD.

Пусть общее решение дифференциального уравнения системы:

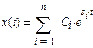, (2.9)

где s - корни характеристического уравнения D(s)=0.

Составляющая этого решения, определяемая степенью устойчивости запишется в виде:

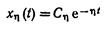(2.10)

для случая вещественных корней или

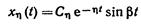(2.11)

для случая, когда среди корней есть пара комплексно-сопряженных.

В большинстве случаев переходный процесс можно считать закончившемся тогда, когда затухнет составляющая переходного процесса, определяемая степенью устойчивости, т.е. порядок величины времени затухания процесса можно грубо оценить по наиболее медленно затухающей составляющей xh(t). В случае, когда ближайшим к мнимой оси является вещественный корень, из (2.10) можно получить следующую зависимость:

t_h = 1/h*ln(1/D). Если принять, например, D=0.05, то время переходного процесса t_h = 3/h. В том случае, когда ближайшей к мнимой оси является пара комплексных корней, из (2.11) можно найти верхнюю границу переходного процесса: t_h = 1/h*ln(1/D).

Можно поставить две задачи:

1. По заданным параметрам системы – коэффициентам D(s) – определить степень устойчивости системы (задача анализа степени устойчивости).

2. По заданной степени устойчивости определить значение варьируемых параметров системы (задача синтеза САУ по заданной степени устойчивости).

Если сместить мнимую ось влево на величину h, тогда один корень окажется на мнимой оси, а система – на границе устойчивости. Это соответствует обращению в нуль старшего определителя Гурвица D_n= a_n*D_n-1 = 0. Это условие дает уравнение, по которому, задаваясь коэффициентами, можно определить h или решить обратную задачу.

Пусть характеристическое уравнение системы:

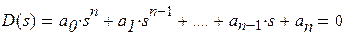
введем новую переменную z = s+h. Подставив значение s = z - h в уравнение D(s) = 0, получим новое смещенное уравнение:

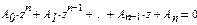, (2.12)

где

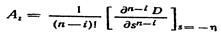(2.13)

Если в смещенном уравнении окажется А_N = 0, то ближайшим к мнимой оси окажется нулевой корень, а если А_n не равно нулю, то пара сопряженных комплексных корней.

Колебательность системы m - тангенс угла, образованный отрицательной вещественной полуосью и лучом из начала координат к корню, у которого отношение мнимой части к действительной максимально.:

m = tg (j) = (b/a)_max , (2.14)

где b - значение мнимой части корней D(s); a - действительная часть.

При известных параметрах системы можно определять значение колебательности m (задача анализа колебательности) или решать обратную задачу – задачу синтеза САУ по заданной колебательности. Для этого в характеристическом уравнении вводится замена s = jze^-jj равноценная повороту мнимой оси на угол (p/2 - j), при этом пара сопряженных комплексных корней окажется на мнимой оси, а фиктивная система – на границе устойчивости. Колебательность m является оценкой переходного процесса сверху, при увеличении m возрастает число колебаний n за время регулирования и возрастает перерегулирование. Реальный переходный процесс может иметь значительно лучшее качество.

Запишем смещенное характеристическое уравнение :

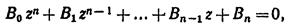(2.15)

где

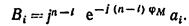(2.16)

в (2.15) часть коэффициентов комплексные числа.

Так как фиктивная система находится на границе устойчивости, то (2.15) имеет пару сопряженных мнимых корней s_i = ±jb_I = ±jw_i.

Если в (2.15) подставить jw вместо z и разделить смещенный характеристический полином на мнимую и действительную части, то их можно поочередно приравнять нулю, получив при этом систему двух уравнений

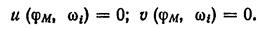
Исключив из этой системы w_i, получим искомое значение j и m = tg j.

Оценка прямых показателей качества переходного процесса – времени регулирования t_p и перерегулирования s по известным h, x, m для любого распределения корней и любых начальных условий пока не найдена. Но для определенных классов распределения корней и начальных условий можно построить две кривые – мажоранту и миноранту, которые ограничивают кривую переходного процесса сверху и снизу:

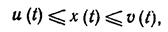
Приведем формулы построения мажорант и минорант без доказательств. Для случая вещественных корней и нулевых начальных условий мажоранта и миноранта описываются соответственно уравнениями:

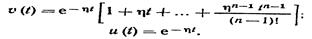(2.17)

Перерегулирование для этого класса корней отсутствует. На рисунке 2.3 показаны кривые u(t) и v(t) для разных степеней уравнения, причем t = ht – относительное время. Чем выше n тем грубее оценка. Если учесть величину x, то можно сблизить миноранту и мажоранту.

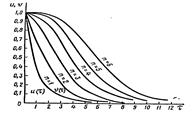
Рисунок 2.3 – Вид мажоранты и миноранты в зависимости от n

Для систем, имеющих среди корней пару комплексно-сопряженных, при тех же начальных условиях мажоранта описывается уравнением (2.17), а миноранта:

u(t) = -v(t) (2.19)

При этом перерегулирование

σ ≤ e^-π/μ (2.20)

Если x(0) = x₀, то s< x₀e^-p/m что проиллюстрировано на рисунке 2.4.

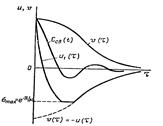
Рисунок 2.4 – Мажоранта и миноранта в случае пары комплексно-сопряженных корней

Используя мажоранту и миноранту, можно оценить время регулирования переходного процесса:

t_u ≤ t_p ≤ t_v

где t_u – время регулирования по миноранте; t_v время регулирования по мажоранте.

Диаграмма Вышнеградского

Рассмотрим характеристическое уравнение третьего порядка:

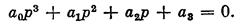(2.21)

Приведем его к нормированному виду. Для этого разделим все члены на а₃ и введем новую переменную

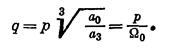(2.22)

Здесь использовано понятие среднего геометрического корня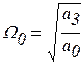

В результате получим нормированное уравнение:

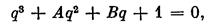(2.23)

где коэффициенты А и В называются параметрами Вышнеградского.

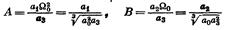
На плоскости параметров А и В нанесем границу устойчивости. Условия устойчивости системы третьего порядка: A > 0; B > 0; AB > 1.Уравнение границы устойчивости (колебательной): AB=1 при A>0 и B>0. Это есть равнобокая гипербола, для которой оси координат служат асимптотами (рисунок 2.5). Область устойчивости этой системы лежит выше кривой.

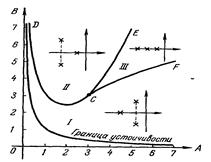
Рисунок 2.5 – Диаграмма Вышнеградского

Разобьем область устойчивости на отдельные части, соответствующие различному расположению корней характеристического уравнения. Заметим, что в точке С, где А=3 и В=3, характеристическое уравнение (2.23) принимает вид (q+1)³=0. Следовательно, в этой точке все три корня равны и равны –1. При этом для исходного характеристического уравнения согласно (2.22) получаем p₁=p₂=p₃= - Ω₀.

В общем случае возможны два варианта: 1)все три корня вещественные; 2) один корень вещественный и два комплексных.

Граница между этими двумя случаями определяется равенством нулю дискриминанта уравнения третьей степени (2.23), который может быть получен, например, из формулы Кардана:

A² B² – 4(A³ + B³) + 18AB – 27 = 0.

Это уравнение дает на плоскости параметров А и В две кривые: CE, CF (рисунок 2.5). Внутри области ECF дискриминант положителен, значит в этой области имеется три вещественных корня (область III). В остальной части плоскости дискриминант отрицателен, что соответствует наличию пары корней. Здесь можно выделить два случая: I – пара комплексных корней лежит ближе к мнимой оси, чем вещественный, и II – вещественный корень лежит ближе к мнимой оси, чем пара комплексных. Границей между этими двумя случаями является расположение всех трех корней на одинаковом расстоянии от мнимой оси. Уравнение этой границы можно найти, положив значения корней q₁ = -α; q_2,3 = - α ± jβ. Подставив это в уравнение (2.23) и приравнивая коэффициенты при одинаковых степенях, получим систему трех уравнений, решив которую получим уравнение:

2A³ – 9AB + 27 = 0, A<3.

Написанное равенство дает на плоскости параметров кривую CD.

В результате область устойчивости разбивается на три части: I, II, III. Этот график называется диаграммой Вышнеградского.

В области III, где все корни вещественные, в зависимости от начальных условий получим апериодический переходный процесс в одной из форм, показанной на третьем графике рисунок 2.6. Область III – область апериодических процессов.

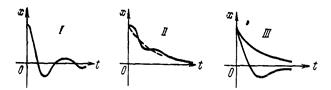
Рисунок 2.6 – Переходные процессы для различных областей диаграммы Вышнеградского

В областях I, II, где имеется один вещественный корень и два комплексных, переходный процесс будет иметь соответственно формы, показанные на первых двух графиках рисунка 2.4. В области I быстрее затухает экспонента и переходный процесс в основном будет определятся колебательной составляющей. Область I – область колебательных процессов. В области II, наоборот, быстрее затухает колебательная составляющая. Область II – область монотонных процессов.