Эвольвентная зубчатая передача. Эвольвента окружности и ее свойства.
Эвольвентная зубчатая передача - цилиндрическая зубчатая передача, профили зубьев которой выполнены по эвольвенте окружности.
Эволютой называется геометрическое место центров кривизны данной кривой. Данная кривая по отношению к эволюте называется эвольвентой. Согласно определению нормаль к эвольвенте ( на которой лежит центр кривизны ) является касательной к эволюте. Эвольвенты окружности описываются точками производящей прямой при ее перекатывании по окружности, которую называют основной.
Свойства эвольвенты окружности:
Форма эвольвенты окружности определяется только радиусом основной окружности rb. При rb → ∞ эвольвента переходит в прямую линию.
Производящая прямая является нормалью к эвольвенте в рассматриваемой произвольной точке My. Отрезок нормали в произвольной точке эвольвенты lMyN = r равен радиусу ее кривизны и является касательной к основной окружности.
Эвольвента имеет две ветви и точку возврата М0, лежащую на основной окружности. Эвольвента не имеет точек внутри основной окружности.
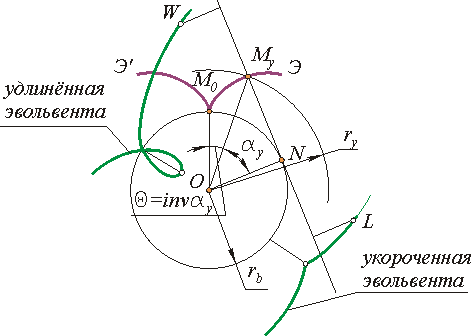
Точки связанные с производящей прямой но не лежащие на ней при перекатывании описывают: точки расположенные выше производящей прямой W - укороченные эвольвенты, точки, расположенные ниже производящей прямой L - удлиненные эвольвенты.
|
| Рис.11.1 |
Параметрические уравнения эвольвенты получим из схемы, изображенной на рис. 11.11 . Так как производящая прямая перекатывается по основной окружности без скольжения то дуга М0N равна отрезку NMy . Для дуги окружности
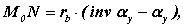
из треугольника D OMyN
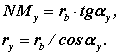
Откуда
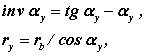
получим параметрические уравнения эвольвенты.
Дата добавления: 2020-02-05; просмотров: 948;











