Угол давления в высшей паре ( на примере плоского кулачкового механизма ).

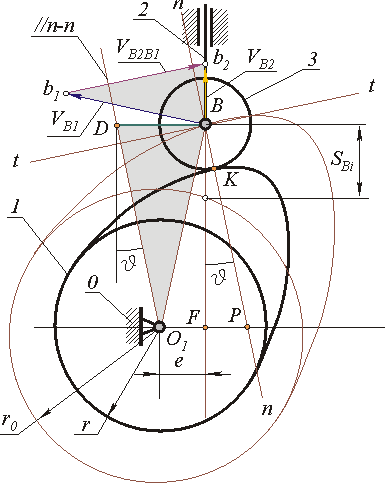
Рассмотрим плоский кулачковый механизм с поступательно движущимся роликовым толкателем ( Рис. 11.9). Из D BPF

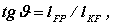
где

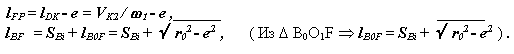
Подставляя эти выражения в формулу для тангенса угла давления, получим

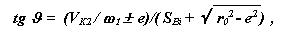
где знак - соответствует смещению оси толкателя (эксцентриситету) вправо от центра вращения кулачка.

 

Рис. 11.9

Формула Эйлера - Савари.

При синтезе плоских зацеплений широко применяется формула Эйлера-Савари, которая устанавливает связь между радиусами кривизны центроид и радиусами кривизны профилей высшей пары. Эта формула записывается так

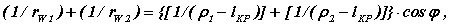
где r_w1 и r_w2 - радиусы кривизны центроид первого и второго звена в полюсе зацепления, ρ₁ и ρ₂ - радиусы кривизны профилей в контактной точке, l_KP - расстояние от полюса зацепления до контактной точки, φ - угол между контактными нормалями к профилям и центроидам.

Теорема Оливье.

Теорема Оливье является основополагающей теоремой как для плоских, так и для пространственных зацеплений. Она устанавливает основные признаки определяющие свойства зацепляющихся поверхностей, вид их контакта друг с другом.

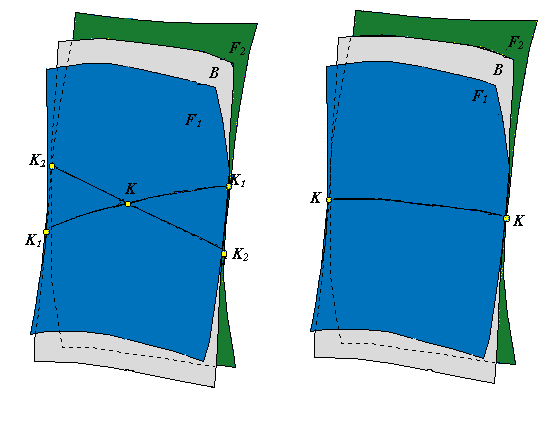
Теорема Оливье. Пусть F₁ , F₂ и B некоторые поверхности с определенным абсолютным движением. И пусть F₁ и F₂ огибающие к B в их относительном движении, где - мгновенные контактные линии. Если K₁ -K₁ и K₂ -K₂ имеют общие точки, то поверхности F₁ и F₂ :

• находятся в точечном контакте, если K₁ -K₁ и K₂ -K₂ пересекаются в некоторой точке K;
• находятся в линейном контакте, если K₁ -K₁ и K₂ -K₂ сливаюся в одну линию, образуя K -K.

Рис. 11.10

Теорема Оливье имеет три важных следствия:

Следствие 1. Если оба зубчатых колеса обработаны друг другом, т.е. первое колесо обработано инструментом режущие кромки которого копируют второе колесо, а второое - инструментом режущие кромки которого копируют первое, то эти колеса имеют взаимоогибаемые поверхности зубьев с линейным контактом поверхностей.

Следствие 2. Если оба колеса обработаны инструментами, образующими между собой конгруентную пару, то эти колеса имеют взаимоогибаемые поверхности зубьев с линейным контактом поверхностей.

Следствие 3. Если поверхность зацепления И₁ инструмента 1 с колесам 1 и поверхность зацепления И₂ инструмента 2 с колесам 2 совпадает с поверхностью зацепления колес 1 и 2, то зубья колес обработанных при таком условии будут иметь линейный контакт.