Интерференция света

Интерференция в тонких пленках

Явление интерференции в тонких пленках широко наблюдается в естественных условиях: радужная окраска мыльных пузырей, нефтяных пленок, масляных пятен на поверхности воды, крыльев бабочки.

В этом случае интерферируют лучи, полученные от отражения падающего луча от верхней и нижней поверхностей. Оптическая разность хода между лучами не велика из-за малой толщины пленки и поэтому они принадлежат одному цугу, а значит когерентны.

Для установления общих закономерностей интерференции света в тонких пленках рассмотрим плоскопараллельную прозрачную пленку толщиной 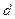, на которую под углом 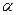= 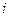падает монохроматическая волна. Будем предполагать, что по обе стороны от пленки находиться воздух. Абсолютный показатель преломления пленки 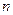больше чем у воздуха.

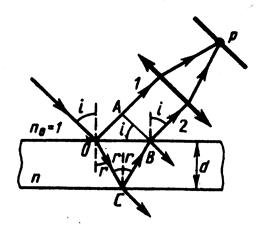Рис.1

Падающая волна частично отражается от поверхности пленки (луч 1) и частично преломляется (луч OC). Преломленная волна, достигнув нижней поверхности пленки, отражается от нее (луч CB). Луч CB затем преломляется на верхней поверхности (луч 2). Лучи 1 и2 с помощью линзы собираются на экране в точке и интерферируют. Результат интерференции зависит от оптической разности хода между лучами 1 и 2.

Оптическая разность хода между двумя интерферирующими лучами от точки O до плоскости AB равна: 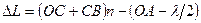, где 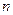- показатель преломления пленки, член 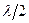обусловлен потерей полуволны при отражении света от границы раздела с оптически более плотной средой. Расстояния OA, OC и CB находится геометрическим методом ( 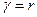, рис.1):

, .

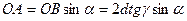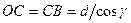Учитывая, что 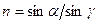, получим:

.

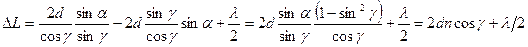Выразим оптическую разность хода через величину угла 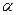. Учитывая, что 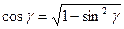, получим:

.

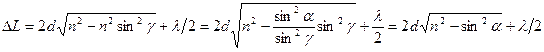Из этого выражения следует, что интерференционная картина в тонких пленках зависит от величин 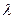, , 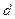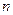и 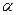. Для заданных 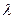, 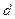и 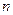каждому наклону лучей 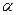соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей падающих на плоско-параллельную пластинку под одинаковыми углами, называются полосами равного наклона (рис.2).

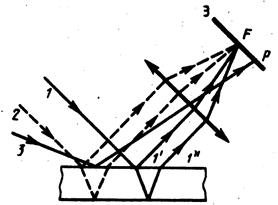Рис.2.

Полосы равной толщины получаются от пластинки переменной толщины. Пусть на клин (угол между боговыми гранями мал) падает плоская волна, направление распространения которой совпадает с параллельными лучами 1 и 2 (рис.3).

Рис.3.

Падающий луч 1 разделяется на луч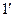и и 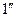, полученные отражением луча от верхней и нижней поверхности клина. После прохождения через линзу лучи пересекутся в точке 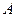, являющейся изображением точки 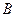. Луч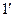и и 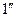когерентны и будут интерферировать в точке 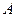. При расчете оптической разности хода толщина клина берется в месте падения луча. Луч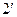и и 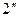, образовавшиеся при делении луча 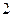, падающего в другую точку клина, собираются линзой в точке 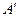. Оптическая разность хода уже определяется толщиной 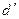. Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину. Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины. Так как верхняя и нижняя грани клина не параллельны между собой то луч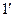и 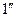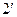и ( и 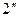) пересекаются вблизи пластинки.

Когда свет падает на кончик клина оптическая разность хода равна 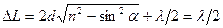, так как 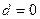. Поэтому кончик клина всегда темный луч 1 теряет 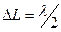а луч2 не теряет .

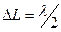Кольца Ньютона

Установка для наблюдения колец Ньютона состоит из плоско-параллельной пластины и плосковыпуклой линзы большого радиуса кривизны. Свет на установку падает вертикально (рис. 4).

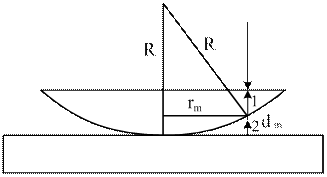Рис. 4

Тонкая пленка образуется между линзой и пластинкой. Это воздушная пленка или жидкая. Пленка имеет вид клина. Поэтому возникают полосы равной толщины. Из-за симметрии они имеют вид окружностей.

Рассмотрим ход одного из лучей. Поскольку угол клина мал, можно считать, что угол падения везде ноль. Когерентными являются лучи, отразившиеся в точках 1 и 2. В точке 1 они накладываются. Найдем радиус 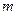-ого кольца .

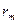Оптическая разность хода между лучами 1 и 2 равна: 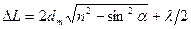. В нашем случае 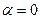, поэтому

.

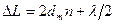Предположим, что кольцо темное, тогда 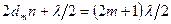. Отсюда выражаем толщину клина в точке 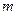кольца :

.

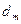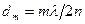Из рис.4 следует, что 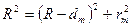. Пренебрегая членом 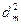, получаем:

.

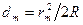Приравнивая оба выражения для 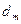, получаем: 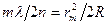. Отсюда выражаем радиус 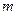-ого темного кольца:

.

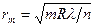Для воздушной пленки ( 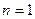), это выражение принимает вид: .

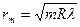Найдем радиусы светлых колец. Оптическая разность хода в этом случае равна 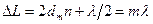. Отсюда 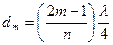. Приравнивая с предыдущим выражением 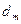, получим:

.

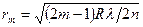Радиусы колец зависят от длины волны 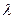, поэтому, если свет немонохроматический, то кольца будут окрашены.

Применение интерференции

1. С помощью колец Ньютона можно определить длину волны, если известен радиус кривизны плосковыпуклой линзы ( ).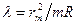

2. Явление интерференции применяется для улучшения качества оптических приборов (просветление оптики). Прохождение света через линзу сопровождается отражением 4% падающего света. Современные объективы содержат до 10 линз, поэтому потери света велики. Отражение от поверхности линз приводит к возникновению бликов, что приводит к демаскировке расположения приборов в военной технике. Для устранения этих недостатков осуществляют просветление оптики. Объектив покрывают пленкой. Ее толщину рассчитывают так, чтобы был интерференционный минимум при наложении лучей (рис. 5).

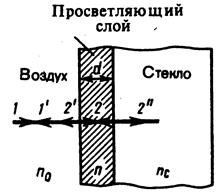Рис.5.

Оптическая разность хода между лучами 1 и 2 равна 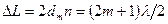. Слагаемое 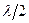отсутствует, так как оба луча отражаются от более плотных поверхностей ( 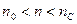). Пленка имеет наименьшую толщину при 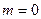. Она равна: 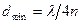. Толщину 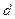подбирают так, чтобы гасить лучи наиболее сильно действующие на глаз (желто-зеленые). Объективы имеют фиолетовый оттенок.