Характеристики синхронного генератора, работающего параллельно с сетью

6.2.1 Угловые характеристики

6.2.2 Синхронизирующая мощность и синхронизирующий момент

6.2.3 V-образные характеристики СГ

6.2.1 Угловые характеристики

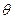
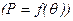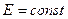Угловой характеристикой активной мощности синхронных машин называется зависимость P и при и 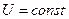. Построим векторную диаграмму синхронного генератора: (положив, что ).

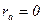Рисунок 6.2.1 – Векторная диаграмма СГ

Спроектируем все вектора напряжений на ось 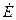, тогда

;

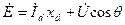(6.2.1)

на перпендикулярное направление:

,

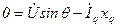(6.2.2)

отсюда

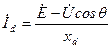,	(6.2.3)
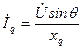.	(6.2.4)

Из векторной диаграммы ясно, что ,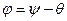

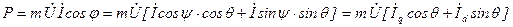
(6.2.5)

Заменив 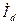и 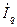выражениями (6.2.3) и (6.2.4), получим

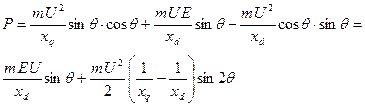
(6.2.6)

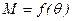Поскольку электромагнитный момент машины , то зависимость имеет тот же вид, что и в выражении (6.2.6)

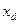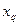В выражении (6.2.6) надо поставлять насыщенные значения и , соответствующие 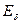, и E, определённое по спрямлённой насыщенной характеристике.

Для анализа положим, что 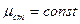, т. е. , .

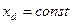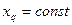Для неявнополюсной машины 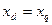, тогда равенство (6.2.6) приобретает вид

.

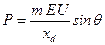(6.2.7)

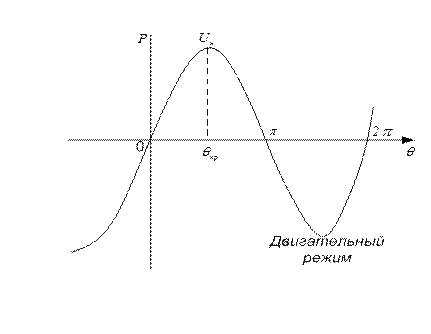
Рисунок 6.2.2 – Угловая характеристика неявнополюсного СГ

Из рисунка (6.2.2) видно, что при 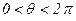− 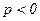, режим работы – двигательный.

Изменение 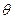означает, что ротор с небольшой скорость проскальзывает относительно поля.

Максимального значения 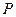достигает при 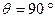, такое значение угла нагрузки называется критическим при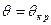

.

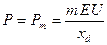(6.2.8)

Из формулы (6.2.8) видно, что P обратно пропорциональна 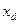, т. е. 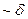, поэтому в синхронных машинах стараются увеличить зазор в точке зрения получения максимальной активной мощности.

В установившимся режиме работы активная мощность, отдаваемая генератором в сеть равна механической мощности 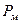приводного двигателя за вычетом механических, магнитных и электрических потерь.

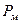не зависит от 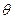, поэтому 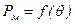− прямая, а рабочая точка определяется пересечением кривых 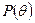и 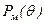, т. е. это точки 1 и 2.

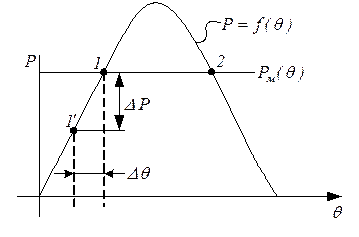
Рисунок 6.2.3 – К определению статической устойчивости СГ

Однако эти точки не равноценны с точки зрения статической устойчивости. Режим работы синхронной машины называется статически устойчивым, если при небольших возмущениях (небольших изменениях U, 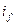, 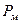) изменения режима работы также будут небольшими, и при прекращении действия этих возмущений восстанавливается прежний режим работы.

Пусть в точки 1 произошло случайное уменьшение 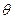на 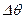, т. е. ротор притормозится, и синхронный генератор будет выдавать меньшую активную мощность, соответствующую точке 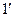, тогда 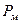окажется большей, чем 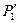, и на валу разовьётся избыточный вращающий момент

,

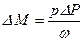(6.2.9)

стремящийся вернуть ротор в точку 1 после прекращения возмущения.

Если в точке 2 увеличится 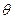на 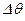, то ротор будет ускорятся ещё больше, так как 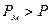, следовательно в точки 2 – режим статически неустойчив.

Таким образом, в области 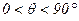синхронный генератор работает устойчиво, а при 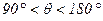− неустойчиво. Общее условие устойчивости выглядит так:

.

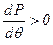(6.2.10)

Невозбуждённая явнополюсная машина

В случае если 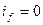, то 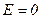и уравнение угловой характеристики приобретёт вид:

,

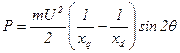(6.2.11)

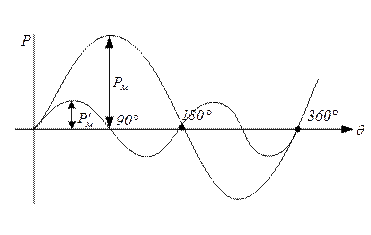
Рисунок 6.2.4 – Угловая характеристика явнополюсного СГ

т. е. при 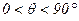машина, потерявшая возбуждение, будет всё равно выдавать активную мощность, причём 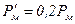и будет развивать электромагнитный момент, называемый реактивным.

В возбуждённой явнополюсной машине кривая 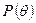будет иметь две составляющие.

6.2.2 Синхронизирующая мощность и синхронизирующий момент синхронной машины

Мы говорили, что в определённых пределах угла 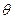машина способна сохранять устойчивость или синхронный режим работы.

Это объясняется тем, что при отклонении θ за счёт разности мощностей синхронной машины и 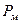возникает 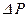, которая и стремится вернуть машину в исходное положение. Эта мощность называется синхронизирующей, а соответствующий ей момент 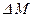- синхронизирующим моментом.

Если 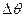мало, то 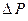и 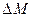прямо пропорциональны этому отклонению, т. е.

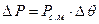,	(6.2.12)
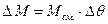,	(6.2.13)

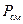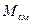где и - соответственно коэффициенты синхронизирующей мощности и момента.

Из (6.2.12) и (6.2.13) получим

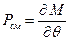,	(6.2.14)
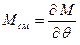.	(6.2.15)

Продифференцировав выражения для P и M по 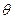, получим

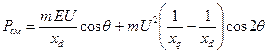
(6.2.16)

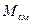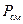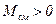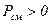Для неявнополюсной и реактивной машины выражения упрощается. Смысл и заключается в том, что при и режим работы синхронной машины – устойчив.

Мы из угловых характеристик видим, что синхронная машина способна развивать максимальную мощность Р_М. Естественно, 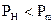, поскольку, во-первых, точка 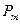находится на границе устойчивости, а во-вторых, напряжение сети может падать. Поэтому синхронная машина всегда должна иметь запас мощности, который характеризуется статической перегружаемостью синхронной машины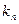

.

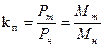(6.2.17)

Обычно .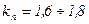

6.2.3 V-образные характеристики синхронной машины

Ранее было выяснено, что изменение тока 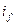ведёт к изменению только реактивной мощности и реактивной составляющей тока якоря. Зависимость тока якоря от тока возбуждения синхронная машина при 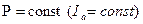графически образует так называемые V-образные кривые.

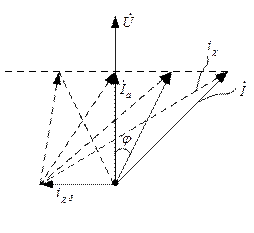
Рисунок 6.2.5 – Упрощенная векторная диаграмма неявнополюсного синхронного генератора

Положим, что синхронная машина работает параллельно с сетью бесконечной мощности, т. е. 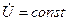. Положим также, что 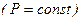, и что 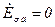, т. е. 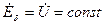и 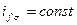. При таких условиях и непрерывном изменени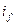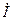и , и 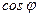также постоянно изменяются. При некотором значении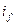 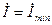, а 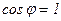, при перевозбуждении ( 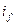возрастает) или недовозбуждении, 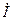растёт, в первом случае отдавая в сеть реактивную мощность, во 2-м – потребляя её из сети.

Минимальная точка каждой кривой 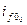определяет

.

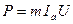(6.2.18)

AB – граница устойчивости, т. е. 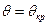, при дальнейшем уменьшении 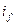машина выпадает из синхронизма.

Кривая 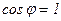(минимумов) с ростом активной мощности Р отклоняется вправо,

т. к. возрастает 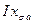, что требует большего 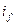для его компенсации.

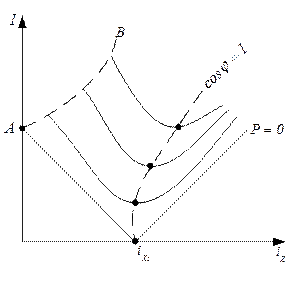
Рисунок 6.2.6 – V-образные кривые синхронного генератора

Минимальная точка каждой кривой 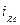определяет

.

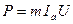(6.2.18)

AB – граница устойчивости, т. е. 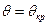, при дальнейшем уменьшении 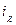машина выпадает из синхронизма.

Кривая 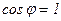(минимумов) с ростом активной мощности отклоняется вправо,

т. к. возрастает 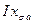, что требует большего 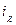для его компенсации.