При мгновенном приложении бесконечной по величине силы возникает жесткий удар, если мгновенно приложена конечная сила – мягкий.

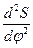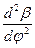Неприятности выявляются при рассмотрении диаграммы ускорения, поэтому функция перемещения толкателя от углового перемещения кулачка обычно выбирается в виде диаграммы изменения второй производной перемещения по углу поворота кулачка или в зависимости от угла поворота кулачка .

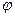Этот параметр (аналог ускорения) пропорционален ускорению толкателя и, при постоянной угловой скорости кулачка, равен произведению квадрата угловой скорости на аналог ускорения. Отсутствие разрывов на этой диаграмме обеспечивает безударность при возникновении инерционной нагрузки передаваемой толкателем кулачку. Нарушение непрерывности приводит к возникновению ударных инерционных нагрузок.

Практика проектирования кулачковых механизмов определила многообразие приемлемых типовых диаграмм изменения второй производной от перемещения толкателя по углу поворота кулачка. Обычно используются, как безударные типы законов движения толкателя, так и законы движения толкателя допускающие «мягкие» удары, когда законы движения толкателя имеют конечные разрывы функции второй производной от перемещения толкателя по углу поворота кулачка.

Типовые законы движения толкателя для краткости дальнейшего изложения обозначим большими буквами русского алфавита как это сделано на рисунке 2.1.

Так как для профилирования кулачка необходимо иметь функцию перемещения толкателя, то выбранный закон движения кулачка в виде функции ускорения (аналога ускорения) необходимо два раза проинтегрировать. При этом нужно иметь ввиду, что при интегрировании мы получим не S, а S-S₀. Интегрировать можно графически [1,2..], а можно получить аналитические выражения.

Все функции, показанные на диаграммах (рисунок 2.1), кусочно-непрерывные. Интегрирование каждого непрерывного куска функции и удовлетворение начальным условиям позволяют определить значения постоянных интегрирования. Тогда результаты интегрирования могут быть представлены выражениями (2.1)...(2.4)

Для толкателя с поступательным движением:

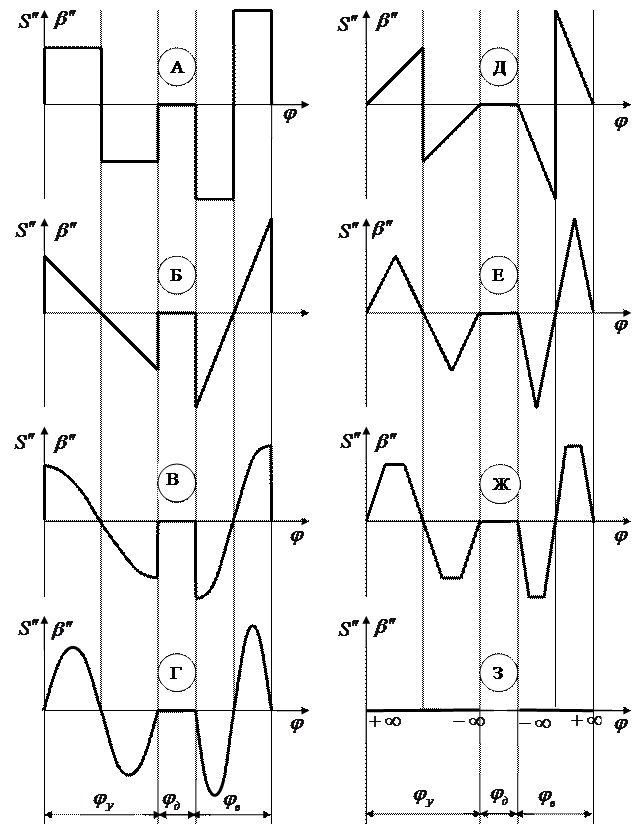Рисунок 2.1. Типовые законы движения толкателя

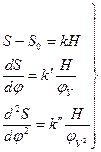
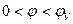(2.1),

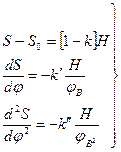
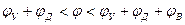(2.2),

Для толкателя, имеющего вращательное движение, зависимости параметров закона движения толкателя от угла поворота кулачка можно представить в виде:

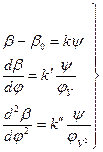
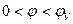(2.3),

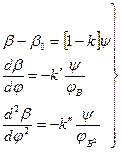
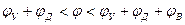(2.4),

Множители 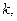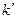, 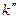в правых частях выражений (2.1)…(2.4) являются функциями угла поворота кулачка. Для целей курсового проектирования достаточно определить значение этих функций в ограниченном количестве точек – 9 точках внутри каждого фазового угла. В таблицах 2.1…2.7 приведены значения этих функций для 9-ти равноотстоящих значений поворота кулачка на отрезках фазовых углов удаления и возвращения толкателя.

Для универсального использования функций коэффициенты 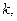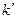, 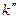приведены для относительных значений угла поворота кулачка к угловой протяженности каждой фазы движения толкателя, то есть в виде

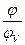и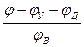

Значения углов в правых частях выражений (2.1)…(2.4) подставляются в радианах.

Таблица 2.1 - Значения коэффициентов 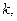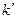, 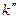параметров закона движения толкателя типа А.

;
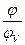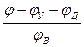
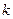
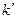
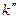
			4,0
1/8	0,03125	0,5	4,0
2/8	0,12500	1,0	4,0
3/8	0,28125	1,5	4,0
4/8	0,50000	2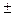,0	4,0
5/8	0,71875	1,5	– 4,0
6/8	0,87500	1,0	– 4,0
7/8	0,96875	0,5	– 4,0
1,0	1,00000		– 4,0

Таблица 2.2 - Значения коэффициентов 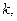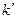, 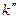параметров закона движения толкателя типа Б.

;
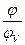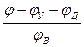
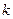
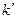
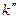
			6,0
1/8	0,04296875	0,65625	4,5
2/8	0,15662500	1,12500	3,0
3/8	0,31640625	1,40625	1,5
4/8	0,50000000	1,50000
5/8	0,68359375	1,40625	– 1,5
6/8	0,84375000	1,12500	– 3,0
7/8	0,95703125	0,65625	– 4,5
1,0	1,00000000		– 6,0

Таблица 2.3 - Значения коэффициентов 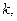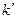, 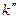параметров закона движения толкателя типа В.

;
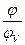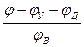
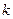
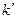
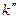
			4,9348020
1/8	0,038006025	0,6011177	4,5591627
2/8	0,146444665	1,1107206	3,4894321
3/8	0,308658300	1,4512266	1,8884669
4/8	0,500000000	1,5707963
5/8	0,691341700	1,4512266	– 1,8884669
6/8	0,853553400	1,1107206	– 3,4894321
7/8	0,961939800	0,6011177	– 4,5591627
1,0	1,000000000		– 4,9348020

Таблица 2.4 - Значения коэффициентов 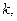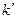, 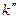параметров закона движения толкателя типа Г.

;
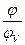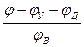
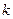
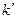
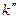
1/8	0,01246047	0,29289330	4,4428826
2/8	0,09084506	1,00000000	6,2831825
3/8	0,26246047	1,70710675	4,4428826
4/8	0,50000000	2,00000000
5/8	0,73753953	1,70710675	– 4,4428826
6/8	0,90915494	1,00000000	– 6,2831825
7/8	0,98753953	0,29289330	– 4,4428826
1,0	1,00000000

Таблица 2.5 -Значения коэффициентов 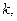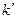, 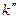параметров закона движения толкателя типа Д.

;
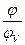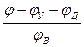
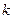
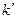
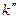
1/8	0,0078125	0,1875	3,0
2/8	0,0625000	0,7500	6,0
3/8	0,2109375	1,6875	9,0
4/8	0,5000000	3,000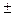0	12,0
5/8	0,7890625	1,6875	– 9,0
6/8	0,9375000	0,7500	– 6,0
7/8	0,9921875	0,1875	– 3,0
1,0	1,0000000

Таблица 2.6 - Значения коэффициентов 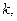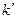, 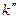параметров закона движения толкателя типа Е.

;
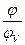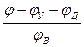
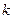
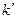
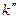
			0,0
1/8	0,010416667	0,25	4,0
2/8	0,083333333	1,00	8,0
3/8	0,260416660	1,75	4,0
4/8	0,500000000	2,00
5/8	0,739583330	1,75	– 4,0
6/8	0,916666670	1,00	– 8,0
7/8	0,989583330	0,25	– 4,0
1,0	1,000000000		0,0

Таблица 2.7 - Значения коэффициентов 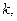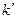, 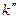параметров закона движения толкателя типа Ж.

;
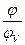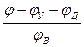
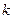
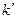
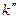
			0,0
1/8	0,013888889	0,3333333	5,3333333
2/8	0,097222222	1,0000000	5,3333333
3/8	0,263888889	1,6666667	5,3333333
4/8	0,500000000	2,0000000	0,0
5/8	0,736111111	1,6666667	– 5,3333333
6/8	0,902777778	1,0000000	– 5,3333333
7/8	0,986111111	0,3333333	– 5,3333333
1,0	1,000000000		0,0