Между двумя несмешивающимися жидкостями

Предположим, в стакане находятся две жидкости, практически не смешивающиеся друг с другом, например, бензол и вода. Введем в эту систему третий компонент, например, небольшое количество йода. Добавленное вещество вполне определенным образом распределится между двумя жидкими фазами. При установлении равновесия в соответствии с теоремой Гиббса химические потенциалы распределяющегося вещества (йода) в соприкасающихся фазах (I) и (II) будут равны:

.

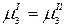Выразим химический потенциал третьего компонента в обеих жидких фазах через его термодинамическую активность:

.

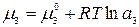Подставим значение химического потенциала:

,

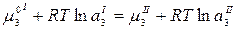где 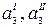– термодинамические активности распределяющегося компонента (йода) в обеих фазах.

Преобразуем:

;

;

.

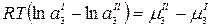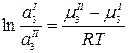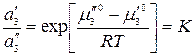Так как стандартный химический потенциал зависит только от температуры, в правой части имеем величину, постоянную при Т = const, тогда

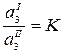
где К – коэффициент распределения вещества между несмешивающимися жидкостями.

Если количество добавленного третьего компонента мало по сравнению с массами фаз, то термодинамические активности можно заменить концентрациями:

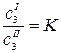. (2.10)

где 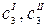– равновесные концентрации распределяющегося вещества в соприкасающихся фазах.

Уравнение (2.10) выражает известный закон распределения Нернста: отношение равновесных концентраций распределяющегося вещества в двух соприкасающихся, но не смешивающихся растворителях есть величина постоянная при Т = const.

Значения К для различных систем приведены в справочной литературе.

Если распределяющийся между фазами компонент в какой-либо из фаз подвержен диссоциации или ассоциации, то закон распределения принимает вид:

,

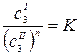где n = const – показатель ассоциации.

Для определения К и n уравнение приводят к линейному виду, логарифмируя правую и левую части:

;

;

.

Рис. 2.9. Графическое определение констант К и n уравнения Нернста

Экспериментально определяют равновесные концентрации распределяемого вещества в обеих фазах, изменяя объемы соприкасающихся фаз или количество вводимого третьего компонента. Затем графически (рис. 2.9) или аналитически определяют n и К.

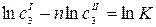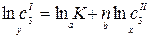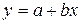Закон распределения Нернста является основой для расчета процесса разделения жидких смесей методами жидкостной экстракции.

Экстракция – процесс извлечения растворенного вещества (целевого компонента) из раствора с помощью другого растворителя (экстрагента), практически не смешивающегося с первым.

Основные цели экстракции:

1. получение чистого растворителя (очистка)

2. концентрирование целевого компонента в аналитических и технологических целях.

Движущая сила экстракции – разность химических потенциалов извлекаемого вещества в растворе и экстрагенте.

При выборе экстрагента сравнивают значения коэффициента распределения, который определяют экспериментально или берут из справочника. Чем больше К, тем эффективнее экстракция при условии, что в законе распределения фазой (I) является экстрагент.

Экспериментально установлено, что лучшее извлечение компонента достигается, если экстракция осуществляется в несколько приемов небольшими порциями экстрагента, чем один раз таким же общим количеством экстрагента. Таким образом, чем больше кратность экстракции, тем эффективнее извлечение целевого компонента.

Раздел III. химическое равновесие