ПЛОСКИХ МЕХАНІЗМІВ.
СИЛОВИЙ АНАЛІЗ (КІНЕТОСТАТИЧНЕ ДОСЛІДЖЕННЯ)
При розв’язуванні задач силового аналізу механізмів передбачаються заданими:
а) закон руху ведучої ланки;
б) маси і моменти інерції механізму.
У тих випадках, коли при розрахунку в число заданих сил не входять сили інерції ланок, розрахунок називається статичним. Розрахунок з урахуванням сил інерції ланок називається КІНЕТОСТАТИЧНИМ.
В основу кінетостатичного розрахунку покладений принцип д'Аламбера відповідно до якого ланка механізму може розглядатися як така, що знаходиться в рівновазі, якщо до всіх зовнішніх сил, що діють на нього, додати сили інерції.
Рівняння рівноваги ланок при цьому називають рівняннями кінетостатики.
Далі, у першому наближенні, будемо вести розрахунок без врахування сил тертя.
1. УМОВА СТАТИЧНОЇ ВИЗНАЧЕНОСТІ КІНЕМАТИЧНИХ
ЛАНЦЮГІВ.
Розглянемо, як будуть спрямовані реакції в кінематичних парах плоских механізмів.
 |
В обертальній парі 5-го класу результуюча сила реакції F проходить через центр шарніра (рис.1). Величина і напрямок цієї реакції невідомі, тому що вони залежать від величини і напрямку заданих сил, прикладених до ланок пар.
У поступальній парі 5-го класу (рис.2) реакція перпендикулярна до осі руху х - х цієї пари. Вона відома по напрямку, але невідома її величина і точка дотику.
У вищій парі 4-го класи реакція F (рис.3) прикладена в точці C торкання ланок 1 і 2 і спрямована по загальній нормалі n - n.
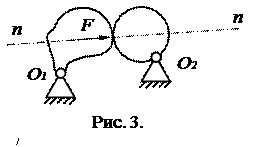 |
Таким чином, для вищої пари 4-го класу нам відомі напрямок реакції і її точки прикладення.
Аналіз вищевикладених ситуацій доводить, що для визначення реакцій у кожній з нижчих пар 5-го класу необхідно визначити по дві невідомих, а для визначення реакції в парі 4-го класу - одну невідому.
На підставі вищевикладеного складемо умову статичної визначеності плоских кінематичних ланцюгів. Для кожної ланки, що має плоско-паралельний рух, можна написати три рівняння рівноваги, то число рівнянь для n ланок - 3n.
Число невідомих для пар 5-го класу - 2Р5, для пар 4-го класу - Р4. Отже, кінематичний ланцюг буде статично визначений, якщо задовольняється умова:
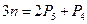 (1)
(1)
Оскільки групи з парами 4-го класу можуть бути замінені групами з
парами 5-го класу, тоді умова статичної визначеності:
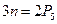 (2)
(2)
звідки
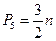 (3)
(3)
але такій умові задовольняють структурні групи Ассура, отже, СТАТИЧНО ВИЗНАЧЕНИМИ кінематичними ланцюгами виявляються СТРУКТУРНІ ГРУПИ АССУРА.
Порядок силового розрахунку є зворотним порядку кінематичного дослідження, тобто силовий розрахунок починається з останньої приєднаної групи і закінчується силовим розрахунком початкової ланки.
2. ВИЗНАЧЕННЯ РЕАКЦІЙ У КІНЕМАТИЧНИХ ПАРАХ
Розглянемо структурну групу 2-го класу 2-го порядку 1-го виду навантажену силами F2, F3 і парами з моментами М2 і М3 (мал.4). Необхідно визначити реакції в кінематичних парах В, C, D. Ця задача може бути вирішена графічним методом планів сил чи аналітично. Розглянемо графічний метод.
У точках В і D прикладаємо невідомі поки що реакції R21 і R34
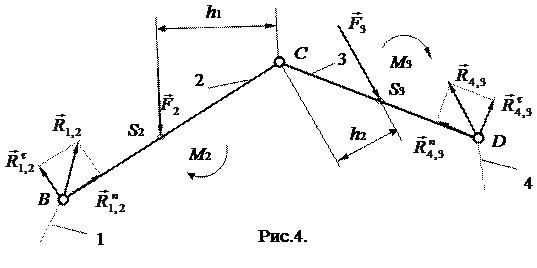
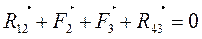 (4)
(4)
 |
Запишемо рівняння рівноваги структурної групи ВСD у векторній формі
Реакції R21 і R43 відомі тільки за точками прикладення. Для їхнього визначення розкладаємо кожну на нормальну і тангенціальну складові, тоді
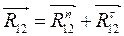 (5)
(5)
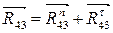 (6)
(6)
Величини тангенціальних складових можуть бути знайдені з рівнянь рівноваги складених для кожної з ланок окремо.
Розглянемо рівновагу ланки 2 у вигляді рівняння моментів усіх сил відносно точки С. Так як знак тангенціальної складової реакції нам невідомий, задаємося довільним. Якщо після визначення цієї величини вона виявиться негативною, то справжній напрямок повинний бути протилежним. Маємо
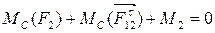 (7)
(7)
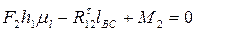 (8)
(8)
звідки
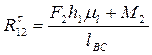 (9)
(9)
Аналогічно з умови рівноваги ланки 3 одержуємо рівняння моментів
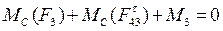 (10)
(10)
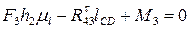 (11)
(11)
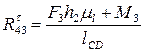 (12)
(12)
Отримані вирази для тангенціальних складових підставляємо у рівняння (4)
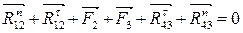 (13)
(13)
У цьому рівнянні невідомими є нормальні складові реакцій, що спрямовані по осях ланок. Величини цих складових можуть бути визначені побудовою плану сил. Для цього з довільної точки а (рис.5) відкладаємо в довільному масштабі mF паралельно самим собі сили, згідно рівнянню (13)
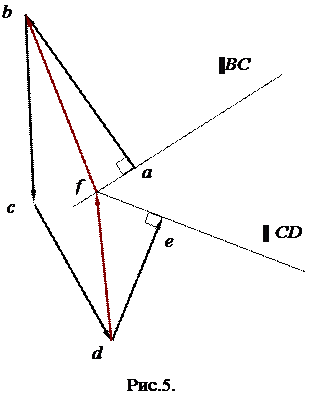 |
Так як нормальна складова реакції прикладеної до другої ланки невідома, план сил починаємо будувати з відомої тангенціальної складової: із точки а відкладаємо вектор тангенціальної складової реакції, довжину (ав) якого визначаємо за формулою
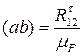 (14)
(14)
де mF – масштабний коефіцієнт плану сил.
Відповідно до векторного рівняння (4) наступним вектором є вектор сили F2 довжину (вс) якого визначаємо аналогічно:
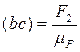 (15)
(15)
Подальші побудови виконуємо аналогічно відповідно рівнянню (4), довжини відповідних векторів визначаємо за формулами:
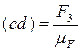 (16)
(16)
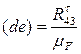 (17)
(17)
Замикання векторного багатокутника робимо так: із точки а проводимо пряму паралельну ланці 2, що відповідає лінії дії нормальної складовий реакції R12, а з точки е – пряму паралельну ланці 3, що відповідає нормальній складовій реакції R43 з боку ланки 4 на ланку 3.
3. Точка f перетину цих прямих є кінцевою точкою вектора (ef), тобто нормальною складовою реакції R43.
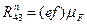 (18)
(18)
Відрізок (fа) у масштабі являє собою нормальну складову реакції R12 .
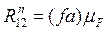 (19)
(19)
1. Силовий розрахунок початкової ланки.
Можуть мати місце два варіанти з’єднання початкової (ведучої) ланки з приводом: 1) з’єднання за допомогою з’єднувальної муфти; 2) з’єднання за допомогою зубчастого зачеплення.
1.1. Розглянемо 1-й випадок, розрахункову схему якого представимо на рис.8,а.
При цьому варіанті момент, що врівноважує (рушійний) передається через з’єднувальну муфту.
 |
У точці В початкової ланки прикладаємо силу R21 орієнтуємо згідно третього закону Ньютона паралельно і протилежно реакції R12. Через те, що ці сили по модулю рівні між собою, визначаємо величину R21:
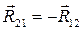 . (30)
. (30)
Момент, що врівноважує, визначаємо з рівняння рівноваги ланки 1:
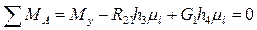 , (32)
, (32)
звідки
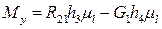 . (33)
. (33)
Для визначення реакції в кінематичній парі А складемо рівновагу ланки у векторній формі:
 . (34)
. (34)
Відповідно до векторного рівняння (34) будуємо план сил (рис. 8,б). Замикаючий вектор проведений у точку а із точки d у масштабі mF і уявляє собою шукану реакцію R01, величину якого визначимо за формулою:
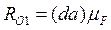 (35)
(35)
1.2. Передача руху здійснюється за допомогою зубчастого зачеплення.
Розрахункову схему представимо на рис.9.
 | |||
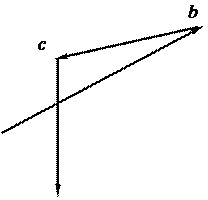 | |||


 | |||||
 | |||||
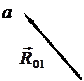 | |||||
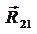
 | |||||
| |||||
|
При цьому варіанті необхідно визначити зрівноважувальну (рушійну) силу в зачепленні Fзр. Для цього складаємо рівняння рівноваги початкової ланки.
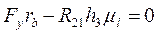 (36)
(36)
звідки визначаємо FY
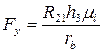 (37)
(37)
Для визначення реакції в кінематичній парі А складаємо умову рівноваги у векторній формі:
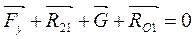 (38)
(38)
Відповідно до рівняння (38) будуємо в масштабі замкнутий багатокутник сил. Шукана реакція визначається у вигляді замикаючого вектора плану сил. Для цього з'єднуємо точку (d) із точкою а. Величину R01 визначаємо за формулою:
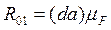 (39)
(39)
| <== предыдущая лекция | | | следующая лекция ==> |
| ДИНАМІЧНЕ ДОСЛІДЖЕННЯ МЕХАНІЗМІВ | | | Основа под живопись |
Дата добавления: 2016-06-15; просмотров: 1854;











