Функционально полные системы логических элементов
Любая комбинационная схема может быть построена с применением лишь трех видов логических элементов: И, НЕ, ИЛИ.
Система элементов, позволяющая строить на их базе логическую схему любой сложности, называется функционально полной системой элементов.
Рассмотрим некоторые функционально полные системы элементов:
1. Система, состоящая из элементов ИЛИ и НЕ ()
2. Система, состоящая з элементов И и НЕ ()
На основании теоремы де Моргана недостающую операцию И или ИЛИ для (1) и (2) можно заменить соответственно на ИЛИ и НЕ.
3. Система, состоящая из одного элемента ИЛИ-НЕ
| _____ |
F = x + y – эта функция называется стрелкой Пирса и обозначается:
| ____ |
F = x ↓ y, то есть x ↓ y = x + y
Функциональная полнота этой системы доказывается тем, что через нее можно выразить все три основные операции булевой алгебры:
а) для операции НЕ (рис.3.4(а))
б) для операции ИЛИ (рис.3.4(б))
в) для операции И (рис.3.4.(в))
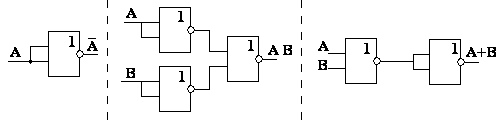
а) б) в)
Рис.3.4.
Имея достаточное количество элементов ИЛИ-НЕ, можно построить логическую схему любой сложности.
4. Система, состоящая из одного элемента И-НЕ
| ___ |
F = xy – эта функция называется «штрих Шеффера» и обозначается:
| ____ |
F = x│y, то есть x│y = x ∙ y
а) для операции НЕ (рис.3.5(а))
б) для операции И (рис.3.5(б))
в) для операции ИЛИ (рис.3.5.(в))
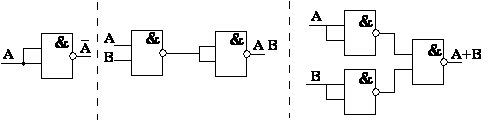
а) б) в)
Рис.3.5.
Минимизация булевых функций с помощью алгебраических
Преобразований
Основная задача минимизации состоит в получении минимальной формы булевой функции, то есть такой формы, которой соответствует логическая схема с минимальным числом элементов.
Для минимизации применяют теоремы булевой алгебры и вытекающие из них свойства булевых функций. Наиболее эффективными являются закон склеивания (теорема 15) и закон поглощения (теорема 13):
15) 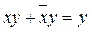
13) х + ху = х
Кроме того, применяется теорема де Моргана; вынесение общих членов за скобки на основании распределительного закона (теорема 12)
а) преобразование путем склеивания:
А*ВС* + А*ВС = А*В(С* + С) = А*В
б) В соответствии с теоремой 3 сумма любого числа одинаковых слагаемых равна этому слагаемому, то есть значение функции не изменится от добавления произвольного числа слагаемых, уже содержащихся в ней. Это свойство используется для создания максимального числа пар для склеивания.
Пример 1
| _ _ _ | |
 х1х2 + х1х2 + х1х2 + х2х3 = х1х2 + х1х2 + х1х2 + х2х3 =
| |
| _ _ _ _ | |
| = х1х2 + х1х2 + х1х2 + х1х2 + х2х3 = | (по теореме 3) |
| _ _ _ | |
| = х2 (х1 + х1) + х1(х2 + х2) + х2х3 = | (по теореме 12а) |
| _ | |
| = х2 ∙ 1 + х1 ∙1 + х2х3 = | (по теореме 4) |
| _ | |
| = х2 + х1 + х2х3 = | (по теореме 6) |
| _ | |
| = х1 + х2 + х2х3 | (по теореме 10а) |
Пример 2
| ________ | |
| х1х2х3х4х5 + х1 + х3х4х5 = | |
| _ _ _ _ _ | |
| = (х1 + х2 + х3 + х4 + х5) + х1 + х3х4х5 = | (по теореме 16г) |
| _ _ _ _ _ | |
| = (х1 + х1) + (х2 + х3 + х4 + х5 + х3х4х5)= | (по теореме 11а) |
| _ _ _ _ | |
| = 1 + (х2 + х3 + х4 + х5 + х3х4х5) = | (по теореме 4) |
| = 1 | (по теореме 2) |
Пример 3
| _ _ _ | |
 F(ABC) = ABC + ABC + ABC + ABC = F(ABC) = ABC + ABC + ABC + ABC =
| |
| _ _ _ | |
| = ABC + ABC + ABC + ABC + ABC + ABC | (по теореме 3) |
| _ _ _ | |
| = BC(A + A) + AC(B + B) + AB(C + C) = | (по теореме 12а) |
| = BC1 + AC1 + AB1 = | (по теореме 4) |
| = BC + AC + AB | (по теореме 6) |
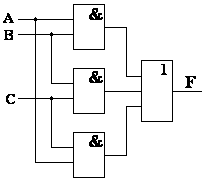
Рис.3.6.
Функции реализуемые схемами рис.3.3. и рис.3.6 одинаковы, однако на рис. 3.6. схема минимизирована.
Дата добавления: 2020-02-05; просмотров: 939;











