Основные теоремы алгебры Буля

<1 2 345 6 7 >

Проектирование экономичных логических схем осуществляется с помощью специального математического аппарата, значительно облегчающего решение этой задачи. Этот аппарат предложен в середине 19-го века английский математик Дж. Буль для использования его в формальной логике и называется алгеброй Буля.

Теорема для одной переменной

1) х + 0 = х	4) х + х* = 1	7) х × х = х
2) х + 1 = 1	5) х × 0 = 0	8) х × х* = 0
3) х + х = х	6) х × 1 = х	9) х** = х

Теорема для двух и более переменных

10)	а) х + у = у + х	}	переместительный закон, имеющий такой же смысл как и в обычной алгебре
б) ху = ух

Теорема справедлива для любого числа переменных. В применении к логическим схемам это означает, что выходной сигнал элементов ИЛИ и И не зависит от того, какие входные сигналы к каким входам элемента подводятся.

y₁=y

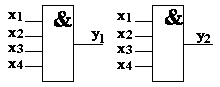
11)	а) х + у + z = x + (у + z) = (x + y) + z	}	сочетательный закон
б) хуz = х × (yz) = (xy) × z

12)	а) х × (у + z) = xу + xz	}	распределительный закон
б) х + уz = (х + y) × (x + z)

Теорема 12б аналога в обычной алгебре не имеет.

13)	а) х + ху = x	}	закон поглощения
б) х × (x + у) = х

Для доказательства теоремы 13а вынесем переменную х за скобки: х × (1 + у) = х в соответствии с теоремами 2 и 6.

14)	а) (х + у*) × у = ху
б) ху* + у = х + у

15)	а) ху + х*у = у	}	закон склеивания
б) (х + у ) × (x* + у) = у

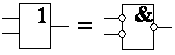
16)	а)	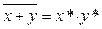	и вообще при любом числе переменных:
б)
в)	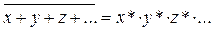}	теорема де Моргана
г)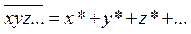

Равенства 16в и 16г означают, что отрицание любого выражения алгебры Буля можно получить заменой всех переменных их отрицаниями, а всех символов логического умножения символами логического сложения и наоборот.