ЭЛЕМЕНТЫ ТЕОРИИ АЛГЕБРЫ ЛОГИКИ.
Лейбниц (Leibniz) Готфрид Вильгельм, немецкий философ, математик, физик, языковед, предвосхитил принципы современной математической логики («Об искусстве комбинаторики», 1666). Создал первую механическую счетную машину, способную производить сложение, вычитание, умножение и деление. Независимо от Ньютона создал дифференциальное и интегральное исчисление и заложил основы двоичной системы счисления Изготовил механический калькулятор, в частности, чтобы облегчить труд своего друга астронома Христиана Гюйгенса.
В машине Лейбница использовался принцип связанных колец суммирующей машины Паскаля, но Лейбниц ввел в нее подвижный элемент (прообраз каретки настольного калькулятора), позволивший ускорить повторение операции сложения, необходимое при перемножении чисел. Вместо колесиков и приводов в машине Лейбница находились цилиндры с нанесенными на них цифрами. Каждый цилиндр имел девять рядов выступов или зубцов. При этом первый ряд содержал один выступ, второй ряд два выступа и так вплоть до девятого ряда, который содержал соответственно девять выступов. Цилиндры с выступами были подвижными и приводились в определенные положения оператором. Специально для своей машины Лейбниц применил систему счисления, использующую вместо обычных для человека десяти цифр две: 0 и 1. Принципы двоичной системы счисления Лейбниц объяснял на примере коробочки с отверстиями: открытое отверстие означало 1, закрытое 0. Единица обозначалась выпавшим шаром, ноль отсутствием выпавшего шара. Двоичная система счисления Лейбница нашла впоследствии применение в автоматических вычислительных устройствах.
Двоичная система счисления основа на простой идеи. Технически легко реализовать элемент в виде реле, например, или транзистора который может принимать всего два значения. В двоичной системе это 0 и 1. Соответственно набором 0 и 1 можно закодировать некоторое количество знаков, чисел. Сколько нулей и единиц может быть всего - это и есть разрядность. То есть, говорят, что ЭВМ 8- разрядная, когда максимальное число, которое может воспринимать ЭВМ - это число из 8 разрядов. Например:
01010000
Соответственно стает вопрос. А сколько всего можно закодировать чисел? Но этот вопрос дает ответ статистика. Сколько будет перестановок из 2 элементов со степенью свободы 8.
28 = 256
Вот это не просто число. Это количество кодируемых символов. Например, в таблице символов ASCII, которая используется для отображения символов всего 256 знаков. И эти знаки нужно распределить среди специальных символов, английских букв и ,например, русских букв. О таблице ASCIIнужно говорить отдельно. И так, как же работать с этой системой счисления. Есть правила математических операций. Так же важен порядок цифр. Первая цифра в двоичной системе «0», а последняя «1». Это правило. Если последняя цифра один, а нужно еще больше, то добавляется новый разряд.
Смотрим:
000 0001 1010 2011 3100 4101 5и так далее.Правила сложения:
0+0=00+1=11+0=11+1=0 (единица переносится в следующий разряд)Правила вычитания:
0 - 0=01 - 0=11 - 1=010 - 1=1 (единица берется из старшего разряда)Попробуем сложить:
011 3010 2------------------101 5Еще:
1001 9
0101 5
------------------
1110 14
А теперь вычитание:
011 3010 2---------001 1
Еще:
101 5
010 2----------011 3Мы заняли единицу из старшего разряда при вычитании.
Правила умножения:
0 • 0=00 • 1=11 • 0=01 • 1=1Пробуем:
10 2 11 3 ---------(10•1) 010(10•1) 10 --------(010+100) 110 6Еще:
11 3
11 3
---------(11•1) 11 (11•1) 11 ----------(011+110) 1001 9Как видите, умножение свелось к сдвигу и сложению.
А деление очень похоже на обычное деление. Это последовательное вычитание делителя из делимого:
1001 (9) : 11 (3)100111 11 11 (3) 11 ------ 0Еще:
101101 (45) : 1001 (9)
1011011001 1 100 10 1001 101 (5) 1001 0
Называемая в честь английского математика Дж. Буля булевой алгеброй, алгебра логики составляет теоретическую основу логики, теории алгоритмов и логического проектирования. От обычной, привычной нам алгебры, булева алгебра отличается тем, что ее логические аргументы (переменные) могут принимать лишь два значения, а основных функций в булевой алгебре всего три: логическое умножение «И», логическое сложение «ИЛИ» и отрицание «НЕ».
Два возможных значения логических переменных называют ИСТИНА (TRUE) и ЛОЖЬ (FALSE), иногда их называют ДА и НЕТ, а чаще всего их обозначают «1» и «0». При этом следует помнить, что эти логические «0» и «1» нельзя трактовать как числа, над ними нельзя производить арифметические действия.
Логическая функция может быть задана четырьмя способами:
– словесно (описанием ситуации),
– алгебраическим выражением,
– таблицей истинности
– электрической схемой, состоящей из контактов переключателей.
Поскольку в цифровых устройствах используются только два символа «0» и «1», алгебра логики использует логические переменные и функции от них, которые также принимают только два значения – «0» и «1».
К более сложным функциям алгебры логики относятся:
- функция равнозначности (эквивалентности)
- функция неравнозначности (сложение по модулю два)
- функция Пирса (логическое сложение с отрицанием)
- функция Шеффера (логическое умножение с отрицанием)
Для булевой алгебры справедливы следующие законы и правила:
- распределительный закон
- правило повторения
- правило отрицания
- теорема де Моргана
- тождества
Схемы, реализующие логические функции, называются логическими элементами. Основные логические элементы имеют, как правило, один выход (Y) и несколько входов, число которых равно числу аргументов (X1;X2;X3 ... XN). На электрических схемах логические элементы обозначаются в виде прямоугольников с выводами для входных (слева) и выходных (справа) переменных. Внутри прямоугольника изображается символ, указывающий функциональное назначение элемента.
В отличие от обычной математики, в алгебре логики операции сложения и умножения заменяют операцией логического умножения, которая звучит красивым словом конъюнкция, и операцией логического сложения - дизъюнкция. Для обозначения операций сложения и умножения используют специальные символы: V - логическое сложение, /\ - логическое умножение, но мы для простоты будет обозначать привычными нам «+» и «х», все равно правильно.
Операция логического сложения обозначается союзом "ИЛИ". Выражение a + b означает "или a или b". т. е. если и a, и b равно нулю, то и результат равен нулю. Результат равен единице, если хотя бы одна из переменных равна единице. Результат также будет единицей, если обе переменных равны единице.
Логическое умножение обозначается союзом "И". Выражение a x b означает "a и b", т. е. если a и b равны нулю, то и результат равен нулю. Если одна из переменных равна единице, другая нулю, то результат все равно равен нулю. Результат равен единице, если обе переменных равны единице. В двух словах все вышесказанное: для логического сложения результат равен нулю только при совпадении нулей, для логического умножения результат равен единице только при совпадении единиц.
Есть еще понятие отрицания, обозначаемое "НЕ". Обозначается отрицание чертой над обозначением переменной или символом «», стоящим перед переменной. Например, ā означает отрицание a. По-другому это отрицание называется инверсией. То есть, если a = 1, то ā = 0 и наоборот. Отрицание может быть не только одной переменной, но и целого выражения.
Понятие двоичной переменной, логических операций И, ИЛИ, НЕ образуют систему аксиом алгебры логики.
Аналогично обычной алгебре, в булевой действительны свойства перестановки, сочетательности и распределительности:
| a + b = b + a |
| a x b = b x a |
| a + (b + c) = (a + b) + c |
| a x (b x c) = (a x b) x c |
| a x (b + c) = a x b + a x c |
Помимо этих есть и другие, свойственные только алгебре логики, законы:
| Законы одинарных элементов |
| a x 1 = a |
| a + 1 = 1 |
| a x 0 = 0 |
| a + 0 = a |
| Законы отрицания (правила де Моргана) |
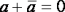
|
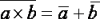
|
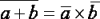
|
| Распределительность дизъюнкции |
| a + (b x c) = (a x b) + (a x c) |
| Правила поглощения |
| a + (a x b) = a |
| a x (a + b) = a |
Эти правила и законы позволяют значительно упростить логические уравнения и функции.
ПРИМЕР:
1. Судовой дизель можно запустить, если включен маслопрокачивающий насос и давление масла в норме, включен топливный насос и давление топлива в норме, клапан на пусковом баллоне открыт и давление пускового воздуха в норме..
2. Если давление масла в норме обозначим как А = 1, давление топлива в норме – В = 1, давление пускового воздуха в норме – С = 1, возможность запуска дизеля обозначить как F = 1, а логическую функцию «И» обозначим знаком умножения " • ", то алгебраическое выражение будет иметь вид :
F = A •B• C
3. В таблицу истинности заносятся все возможные комбинации входных аргументов и соответствующие этим комбинациям значения выходной функции. Входные комбинации записываются в порядке возрастания их значений от всех нулей до всех единиц сверху вниз. Таблица истинности, соответствующая данному примеру будет иметь следующий вид:
А В С F
––––––––––––––––––
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
4. Электрическая контактная схема обладает хорошей наглядностью, но может быть легко построена лишь для самых простых логических функций. Для нашего примера эта схема может иметь следующий вид:
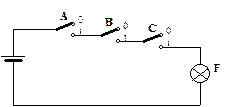
Рисунок 1.1. Электрическая контактная схема
Дата добавления: 2020-02-05; просмотров: 865;











