ПАРАМЕТРЫ СОСТОЯНИЯ СИСТЕМЫ

Каждое конкретное состояние термодинамической системы может быть охарактеризовано рядом величин, которые называются термодинамическимипараметрами.

Если значение параметров системы во всех точках ее объема одинаково, такая система называется равновесной. Математический аппарат классической термодинамики, строго говоря, применим лишь к таким состояниям.

Одна часть параметров может быть непосредственно измерена простыми техническими средствами. Эти параметры называют основными. Другая часть находится расчетным путем с помощью основных параметров состояния.

В термодинамике в качестве основных параметров состояния используются: абсолютное давление, абсолютная температура и удельный объем.

Абсолютное давление – это сила, действующая по нормали к поверхности и отнесенная к единице площади этой поверхности.

В качестве единиц измерения давления используются:

1. Техническая атмосфера 1ат = 1 .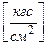

2. Физическая атмосфера. Одна физическая атмосфера эквивалентна давлению, которое оказывает столб ртути высотой 760 мм при t = 0 ⁰С.

3. Паскаль 1Па = ;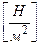

4. Бар 1бар = ;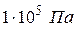

5. Миллиметры ртутного столба мм.рт.ст.

6. Миллиметры водного столба мм.вод.ст.

В системе СИ единицей измерения давления является Паскаль (Па).

Следует напомнить, что кроме барометров, все приборы для измерения давления фиксируют разницу между измеряемым абсолютным давлением Р и давлением окружающей среды Р_о.

Р = Р_м + Р_о , где Р_м – показания манометра.

Если абсолютное давление ниже давления окружающей среды (вакуум), то

Р = Р_о - Р_вак , где Р_вак – показания вакуумметра.

Абсолютная температура Т является важнейшим параметром состояния. Она характеризует тепловое состояние тела.

Т, К; t, ⁰С; Т = t + 273.

Удельный объем – это объем, занимаемый единицей массы вещества, составляющего систему.

Если принять, что масса системы m кг, ее объем V м³, то удельный объем:

v = 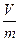м­³/кг.

Вместо удельного объема можно оперировать понятием плотность. Плотностью вещества ρ называют массу вещества, заключенную в единице объема:

ρ = m / v кг/м­³.

Для равновесной, однородной термодинамической системы существует определенная аналитическая зависимость между основными параметрами состояния:

f (P, v ,T) = 0, (2.1)

которая называется уравнением состояния.

Из уравнения (2.1) следует, что независимыми параметрами могут быть лишь два каких-либо параметра, которые и определяют значение третьего.

В наиболее простом случае:

Р V_μ = R_μ T, (2.2)

где V_μ – объем моля газа (при н.у. V_μ = 22,4 м³);

R_μ = 8314 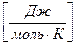– универсальная газовая постоянная.

Газ, для которого справедливо уравнение (2.2) называется идеальным. Модель идеального газа представляет собой газ, молекулы которого рассматриваются как материальные точки, взаимодействие которых между собой ограничено упругими соударениями.

Для 1кг идеального газа уравнение состояния имеет вид:

Р v = R T, (2.3)

где 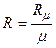– газовая постоянная .

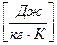Газовая постоянная (в отличие от универсальной газовой постоянной) является характеристикой для каждого газа постоянной, численно равной отношению универсальной газовой постоянной (R_μ)к массе моля данного газа ( μ). Величину R иногда называют характеристической газовой постоянной.

Если в результате взаимодействия с окружающей средой меняется хотя бы один из параметров состояния системы, то говорят об изменении ее состояния.

Изменение состояния системы, характеризующееся изменением ее термодинамических параметров, называют термодинамическим процессом.

Все процессы, происходящие в термодинамической системе, можно разделить на равновесные и неравновесные.

Равновесный процесс представляет собой непрерывный ряд равновесных состояний.

Большую роль в термодинамике играют понятия – обратимые и необратимые процессы.

Обратимым называется процесс, после которого система и окружающая среда могут возвращаться в начальное состояние. Обратимыми могут быть лишь равновесные процессы.

В реальных условиях обратимых процессов не существует. Все реальные процессы необратимые. Типичным примером необратимого процесса является процесс трения. Работа, затрачиваемая на преодоление трения, необратимо превращается в тепло.

Классический аппарат термодинамики применим лишь к равновесным обратимым процессам.

Все параметры термодинамической системы (в том числе и ранее рассмотренные P, v и T) отличаются той особенностью, что их изменение не зависит от вида процесса, а целиком определяется начальным и конечным состоянием системы, т.е. любой параметр – функция состояния.

Кроме перечисленных ранее основных параметров состояния (P, v и T), в термодинамике исключительно важную роль играют следующие параметры состояния: внутренняя энергия, энтальпия и энтропия.

Внутреннюю энергию системы в термодинамике рассматривают как сумму кинетической энергии составляющих ее частиц и потенциальной энергии, обусловленной их взаимным притяжением.

Внутренняя энергия всей системы обозначается U, [Дж], а отнесенная к единице массы u, .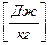

Как известно из физики, кинетическая энергия частиц однозначно связана с абсолютной температурой.

Потенциальная энергия системы при прочих равных условиях определяется расстоянием между частицами, которое в интегральной форме может характеризоваться удельным объемом.

Таким образом:

U = U (T, v).

В идеальном газе отсутствует взаимное притяжение между частицами, поэтому его внутренняя энергия не зависит от объема и включает в себя лишь кинетическую составляющую:

U = U (T).

Энтальпия – это функция состояния (параметр состояния), представляющая собой сумму внутренней энергии и произведения абсолютного давления на объем.

Энтальпия всей системы равна:

Н = U + PV.

Энтальпия, отнесенная к 1 кг массы системы:

h = u + Рv.

В термодинамике для обозначения энтальпии иногда используют букву I – для обозначения энтальпии всей системы и i – для обозначения удельной энтальпии, т.е. H 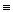I, a h 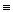i.

Энтропия – это функция состояния системы (S), определяемая тем, что ее дифференциал при элементарном равновесном процессе (dS) равен отношению бесконечно малого количества теплоты (dQ), сообщенной системе, к абсолютной температуре системы.

Энтропия всей системы равна

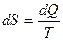. (2.4)

Энтропия, отнесенная к 1 кг массы системы

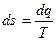. (2.5)

Энтальпия и энтропия, являясь параметрами состояния системы, могут быть, как и внутренняя энергия, представлены в виде функции любых двух других параметров состояния. Например

h = h (p,T);

s = s (p, v).