Вариационных рядов распределения
Для наглядного изображения дискретных вариационных рядов распределения строят три вида графиков – полигон частот, кумулятивную кривую и огиву.
Полигон частот представляет собой ломаную кривую, соединяющую точки, координатами которых являются по оси абсцисс – варианты группировочного признака, а по оси ординат – соответствующие им частоты. Такая кривая наглядно характеризует форму распределения единиц статистической совокупности по величине группировочного признака. При этом самой высокой вершине полигона частот соответствует модальное значение группировочного признака.
При построении кумулятивной кривой по оси ординат вместо частот откладывают накопленные частоты. Это позволяет наглядно отразить изменение концентрации вариантов группировочного признака. Если поменять местами оси координат, то кумулятивная кривая преобразуется в другой вид графика – огиву.
Пример 4.3. В таблице 4.6 (первая и вторая строки) представлено распределение числа рабочих бригады (f) по величине квалификационного разряда (х).
Таблица 4.6
| x | ||||||
| f | ||||||
| S |
Изобразим представленный ряд распределения в виде полигона частот (рис.4.1).
 |
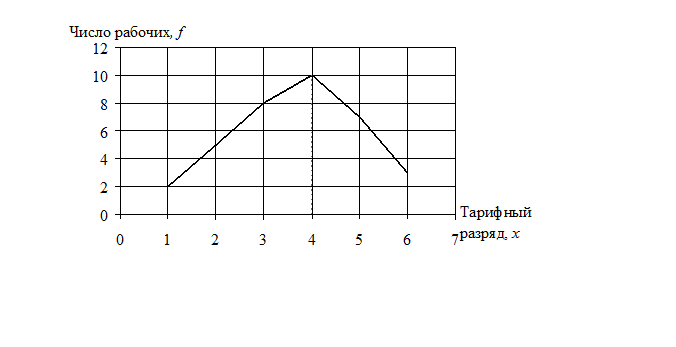
Рис. 4.1
Обозначим S - накопленное число рабочих и рассчитаем значения третьей строки таблицы 4.6. Тогда изображение исследуемого ряда распределения рабочих по величине тарифного разряда в виде огивы имеет следующий вид (рис. 4.2).
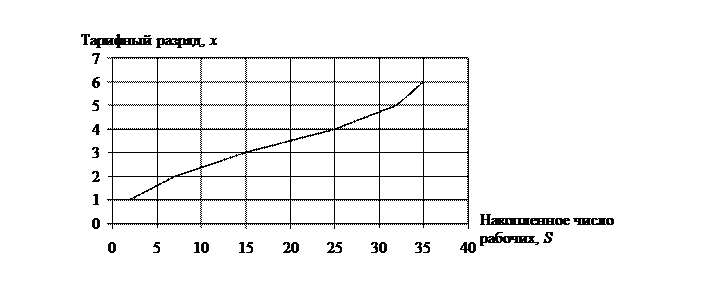
Рис. 4.2
Форма распределения единиц статистической совокупности в интервальном вариационном ряду изображается с помощью гистограммы – разновидности столбиковой диаграммы. Она строится по аналогии с полигоном частот, но вместо вариантов группировочного признака на оси абсцисс указываются его интервалы.
Пример 4.4. Построим гистограмму на основе исходных данных, представленных в таблице 4.4.
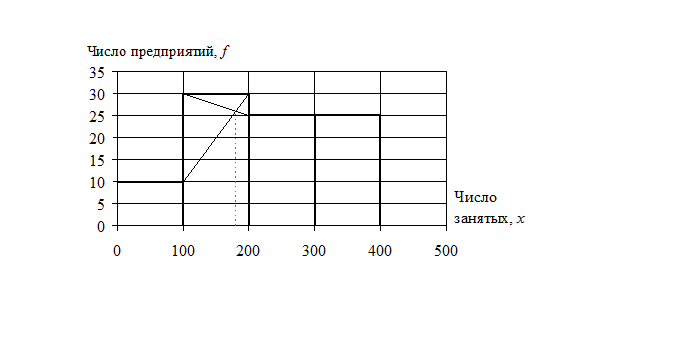
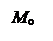 |
Рис. 4.3
Самый высокий столбец гистограммы (рис. 4.3) соответствует модальному интервалу. Если соединить крестом вершины этого столбца с соседними столбцами и из пересечения опустить перпендикуляр на ось абсцисс, то получим значение моды. В нашем случае оно примерно равно 180 чел., что подтверждается сделанным ранее расчетом (см. пример 4.1).
В рассмотренном примере интервалы группировочного признака имеют равную ширину. Если это условие не соблюдается, то использовать при построении гистограммы значения частот нельзя, так как это искажает реальную форму статистического распределения. В этом случае по оси ординат вместо значений частот необходимо указывать значения плотности распределения.
Пример 4.5. Построим гистограмму на основе исходных данных, представленных в таблице 4.5.
Как видно из графика (рис. 4.4), чаще всего в рамках исследуемой статистической совокупности встречаются предприятия с балансовой прибылью от одного до двух млн. руб.
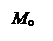 |
Рис. 4
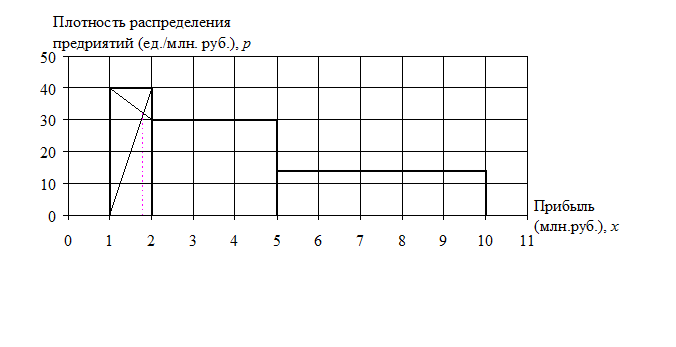
Графическое определение моды при неравных интервалах проводится так же, как и при равных интервалах. В нашем случае ее значение составляет примерно 1,8 млн. руб., что подтверждается сделанным ранее расчетом (см. пример 4.2).
Дата добавления: 2022-07-20; просмотров: 176;











