Статистическая группировка
Статистическая группировка заключается в разделении единиц статистической совокупности на однородные группы по существенным для них признакам. Например, разделение организаций на группы по форме собственности, виду выпускаемой продукции, величине товарооборота или балансовой прибыли.
По типу решаемых задач статистические группировки делятся на:
· типологические – для выделения качественных типов внутри явления;
· структурные – для изучения структуры явления и характеризующих его признаков в зависимости от значения группировочного признака;
· аналитические – для выявления связей между признаками, характеризующими явление.
Например, представленная в таблице 1 статистическая группировка позволяет выделить два качественных типа квартир – муниципальные и частные.
На основе данных наблюдения квартир жилого дома может быть построена структурная группировка (таблица 3.2), характеризующая структуру квартир дома по числу комнат и структуру жильцов дома по числу комнат.
Таблица 3.2
| Число комнат в квартире | Число квартир | Число жильцов, чел. | ||
| всего | % к итогу | всего | % к итогу | |
| Итого |
Те же данные наблюдения могут быть сгруппированы аналитически (таблица 3.3). В этом случае группировка позволяет проанализировать зависимость числа жильцов в одной квартире жилого дома от числа комнат в ней.
Таблица 3.3
| Числа комнат в квартире | Число квартир | Среднее число жильцов в одной квартире |
| Итого | - |
Группировка по одному признаку называется простой (таблицы 3.1, 3.2, 3.3), по двум и более – сложной. Сложные группировки бывают комбинационными и многомерными.
При комбинационной группировке группы, образованные по одному признаку, делят на подгруппы по второму признаку и т. д. Итоги при этом подсчитывают в обратном порядке. Пример комбинационной группировки с двумя группировочными признаками представлен в таблице 3.4.
При многомерной группировке единицы группируются одновременно по нескольким признакам. Например, группировка предприятий по форме собственности и числу занятых в двумерном варианте выглядит следующим образом (таблица 3.5).
Таблица 3.4
| Форма собственности предприятия | Число занятых, чел. | Число организаций |
| Хозяйственные товарищества и общества | до 100 | |
| свыше 100 | ||
| итого | ||
| Производственные кооперативы | до 100 | |
| свыше 100 | ||
| итого | ||
| Государственные и муниципальные унитарные предприятия | до 100 | |
| свыше 100 | ||
| итого | ||
| Всего |
Таблица 3.5
| Форма собственности предприятия | Число занятых, чел. | Итого | |
| до 100 | свыше 100 | ||
| Хозяйственные товарищества и общества | |||
| Производственные кооперативы | |||
| Государственные и муниципальные унитарные предприятия | |||
| Итого |
В общем случае построение многомерных группировок сродни представлению многомерного пространства. Двумерное пространство изобразить очень легко, трехмерное – чуть сложнее. А вот начиная с четырехмерного пространства, сделать это без потери наглядности и легкости восприятия невозможно. По этой причине многомерные группировки в общем случае создаются не в ручную, а с использованием ЭВМ.
Построение группировок по количественному признаку
Если группировочный признак является количественным и дискретным с ограниченным числом вариантов его значений, то единицы наблюдения разбивают на группы по этим вариантам. Например, группировка рабочих предприятия по вариантам квалификационного разряда.
Если число дискретных вариантов велико, то их объединяют в интервалы. Также поступают, если признак является непрерывным, то есть принимает любые значения в заданных пределах.
При определении числа группировочных интервалов и их ширины руководствуются следующим правилом. Чем больше объем наблюдаемых единиц и/или сильнее вариация группировочного признака, тем больше должно быть интервалов и меньше их ширина. Выполнение этого правила обеспечивает попадание в каждый интервал достаточного числа единиц наблюдения и повышает точность последующих расчетов.
При большом числе единиц наблюдения число интервалов определяют по формуле Стерджесса
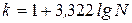 ,
,
где:
k – число интервалов;
N – число единиц наблюдения (N > 30).
Интервалы группировочного признака могут быть равными и неравными. Равные интервалы применяют при незначительной вариации признака и определяют по формуле:
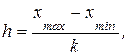
где:
h – ширина интервала группировочного признака;
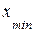 – минимальное значение группировочного признака;
– минимальное значение группировочного признака;
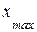 – его максимальное значение.
– его максимальное значение.
Если закон распределения единиц наблюдения по величине группировочного признака является нормальным, то полагают, что:
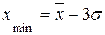 ;
; 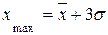 ,
,
где:
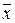 – среднее значение группировочного признака;
– среднее значение группировочного признака;
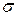 –среднеквадратичное отклонение отдельных значений группировочного признака от его среднего значения.
–среднеквадратичное отклонение отдельных значений группировочного признака от его среднего значения.
В этом случае формула расчета ширины интервалов преобразуется к виду:
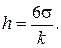
Пример 3.1. Известно, что для 1000 предприятий среднее число занятых составляет 300 чел. при среднеквадратичном отклонении 11 чел. Определим границы интервалов для группировки предприятий по числу занятых.
Решение.
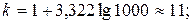
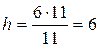 чел.;
чел.;
xmin = 300 – 3 ∙ 11 = 267 чел.;
267 – 273; 273 – 279; 279 – 285; 285 – 291; 291 – 297;
303 – 309; 309 – 315; 315 – 321; 321 – 327; 327 – 333 чел.
Если вариация группировочного признака значительна, то используют неравные по ширине интервалы, изменяющиеся в арифметической или геометрической прогрессии.
При арифметической прогрессии для расчета ширины интервалов используют формулу:
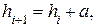
где:
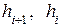 – величина (i+1)-го и i-го интервалов;
– величина (i+1)-го и i-го интервалов;
a – const (если интервалы возрастают, то а > 0, если убывают – a < 0).
Примером использования неравных арифметически возрастающих интервалов является группировка предприятий по объему выручки от реализации продукции (тыс. руб.): 500 – 800; 800 – 1300; 1300 – 2000; 2000 – 2900; 2900 – 4000. Здесь при расчете ширины интервалов был использован параметр а = 200 тыс. руб.
При геометрической прогрессии используется другая формула:
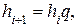
где q – положительная const (при q > 1 интервалы возрастают, при q < 1 – убывают).
В рассмотренной группировке предприятий по объему выручки от реализации имеется неопределенность. Например, не ясно, в какой интервал попадет предприятие с выручкой в 2 млн. руб. – в третий или в четвертый? В подобных случаях из «спорных» интервалов исключают одну из границ – левую или правую (единообразно для всех интервалов). Для этого рядом с правой границей первого интервала ставят знак «+» или знак «–» соответственною. Например, указание «500 – 800 (+)» означает, что все правые границы входят в интервалы, а левые – не входят (за исключением первого интервала).
При дискретном группировочном признаке обходятся без таких знаков. Например, при группировке предприятий по числу занятых (чел.) с неравными геометрически возрастающими интервалами с параметром q=2:
50 – 100; 101 – 200; 201 – 400; 401 – 800; 801 – 1600.
Границы интервалов группировочного признака могут быть закрытыми, как в рассмотренных ранее группировках, и открытыми, например, «до 100 чел.» или «801 чел. и более». При последующих расчетах ширину открытых интервалов определяют исходя из общей тенденции изменения ширины интервалов в рамках всей группировки.
Пример 3.2. В таблице 3.6 представлены данные статистического наблюдения коммерческих банков. Проведем статистическую сводку представленных данных на основе структурной группировки банков по величине капитала.
Таблица 3.6
| Порядковый номер банка | ||||||||||
| Капитал, млн. руб. | 5,0 | 4,9 | 51,4 | 62,0 | 50,1 | 20,3 | 16,7 | 9,4 | 53,0 | 31,3 |
| Работающие активы, млн. руб. | 7,3 | 7,5 | 73,3 | 92,0 | 81,4 | 33,5 | 20,9 | 12,5 | 78,3 | 45,4 |
| Порядковый номер банка | ||||||||||
| Капитал, млн. руб. | 35,6 | 3,5 | 15,0 | 5,6 | 3,2 | 16,6 | 18,4 | 19,7 | 24,2 | 5,0 |
| Работающие активы, млн. руб. | 45,0 | 4,6 | 20,1 | 7,6 | 4,0 | 21,3 | 25,0 | 23,6 | 30,5 | 7,5 |
| Порядковый номер банка | ||||||||||
| Капитал, млн. руб. | 20,4 | 7,8 | 60,5 | 26,6 | 10,5 | 10,4 | 11,3 | 37,9 | 16,2 | 2,0 |
| Работающие активы, млн. руб. | 27,6 | 10,5 | 90,3 | 36,6 | 13,0 | 12,5 | 14,9 | 40,5 | 20,9 | 3,6 |
Решение.
Вначале определим количество групп в будущей статистической группировке и ширину интервалов группировочного признака:
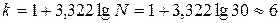 :
:
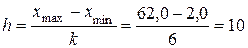 млн. руб.
млн. руб.
Тогда интервалы группировочного признака состаляют:
2 – 12 (+); 12 – 22; 22 – 32; 32 – 42; 42 – 52; 52 – 62 млн. руб.
Сгруппируем банки по интервалам капитала, подсчитываем для каждой группы число банков и итоговое значение работающих активов (таблица 3.7).
Таблица 3.7
| № п/п | Группы банков по величине капитала, млн. руб. | Число банков | Работающие активы | ||
| всего, ед. | % к итогу | всего, млн.руб. | % к итогу | ||
| 2 – 12 (+) | 40,00 | 105,5 | 11,53 | ||
| 12 – 22 | 26,66 | 192,9 | 21,09 | ||
| 22 – 32 | 10,00 | 112,5 | 12,30 | ||
| 32 – 42 | 6,67 | 88,5 | 9,68 | ||
| 42 – 52 | 6,67 | 154,7 | 16,91 | ||
| 52 – 62 | 10,00 | 260,6 | 28,49 | ||
| Итого | 100,00 | 914,7 | 100,00 |
Как видно из таблицы, в структуре коммерческих банков преобладают банки с величиной капитала до 32 млн. руб. Их число составляет 76,66 % от всех банков. При этом на долю этих банков приходится значительная часть рабочих активов – 44,92 %.
Пример 3.3. Преобразуем полученную статистическую сводку в сводку на основе аналитической группировки (таблица 3.8) с целью последующего изучения зависимости величины работающих активов банка от размера его капитала.
Решение.
На основе уже полученных данных заполним часть граф таблицы 3.8 и рассчитаем недостающую информацию.
Таблица 3.8
| № п/п | Группы банков по величине капитала, млн. руб. | Число банков | Капитал, млн.руб. | Работающие активы, млн.руб. | ||
| всего | в среднем на один банк | всего | в среднем на один банк | |||
| 2 – 12 (+) | 78,6 | 40,00 | 105,5 | 11,53 | ||
| 12 – 22 | 143,3 | 26,66 | 192,9 | 21,09 | ||
| 22 – 32 | 82,1 | 10,00 | 112,5 | 12,30 | ||
| 32 – 42 | 73,5 | 6,67 | 88,5 | 9,68 | ||
| 42 – 52 | 101,5 | 6,67 | 154,7 | 16,91 | ||
| 52 – 62 | 175,5 | 10,00 | 260,6 | 28,49 | ||
| Итого | 654,5 | 100,00 | 914,7 | 100,00 |
Как видно из таблицы 3.8, имеет место прямая зависимость величины работающих активов банка от размера его капитала, то есть чем выше уровень капитализации банка, тем больше значение его работающих активов. Для более подробного анализа этой зависимости (оценки ее формы и силы) необходимо использовать методы корреляционного анализа, которые будут рассмотрены в главе 8 данного учебного пособия.
Вторичная статистическая группировка
При сравнении однотипных группировок на основе одного и того же группировочного признака, но отличающихся числом и размером его интервалов, эти группировки предварительно приводят к сопоставимому виду. Для этого за основу берут интервалы группировочного признака одной из группировок, а для другой проводят вторичную группировку.
В основе вторичной статистической группировки лежит правило – в какой пропорции перераспределяются старые интервалы между новыми, в такой же пропорции перераспределяются между ними единицы наблюдения. Это значит, что если вновь установленный интервал включает в себя какой-либо из старых, то за ним закрепляют все единицы этого старого интервала. Если он включает в себя часть старого интервала, то за ним закрепляют долю единиц пропорционально включаемой части. При этом перераспределение единиц наблюдения влечет за собой пропорциональное этому перераспределение итоговых значений статистических признаков между новыми группами единиц наблюдения.
Пример 3.4. В таблице 3.9 представлены данные структурной группировки акционеров по размеру дивидендов. Проведем вторичную группировку акционеров на основе новых интервалов: 50 – 100; 100 – 200; 200 – 400 тыс. руб.
Таблица 3.9
| № п/п | Группы акционеров по размеру дивидендов, тыс. руб. | Число акционеров, % к итогу |
| 50 – 100 | ||
| 100 – 150 | ||
| 150 – 250 | ||
| 250 – 400 | ||
| Итого |
Решение.
Порядок вторичной группировки и ее результаты представлены в таблице 3.10. В соответствие с заданием первый интервал первоначальной группировки остаётся неизменным, второй объединяется с половиной третьего, а оставшаяся половина третьего интервала объединяется с четвёртым. При этом акционеры перераспределяются пропорционально перераспределению интервалов.
Таблица 3.10
| № п/п | Группы акционеров по размеру дивидендов, тыс. руб. | Число акционеров, % к итогу | ||
| Старые | Новые | Старое | Новое | |
| 50 – 100 | 50 – 100 | |||
| 100 – 150 | 100 – 2000 | 20+½ .30=35 | ||
| 150 – 250 | 200 – 400 | ½ .30+30=45 | ||
| 250 – 400 | – | – | ||
| Итого |
Необходимо отметить, что способ вторичной группировки основан на предположении, что единицы наблюдения в рамках каждого из интервалов распределены по величине группировочного признака равномерно. Как правило, это не соответствует реальным первичным данным статистического наблюдения и влечет за собой некоторую неточность последующего сравнения группировок. Однако возможность не возвращаться к обобщению первичных данных, особенно при их значительном объеме, существенно сокращает подготовительный этап проведения процедуры сравнения.
Дата добавления: 2022-07-20; просмотров: 442;











