Средние статистические показатели

Средние величины являются наиболее распространенной формой статистических показателей, используемых в социально-экономических исследованиях. Их расчет основан на осреднении отдельных значений статистических признаков. В результате получаются обобщенные количественные характеристики исследуемого явления по каждому из характеризующих его признаков.

Важнейшее свойство средних статистических показателей заключается в том, что они отражают то общее, что присуще всем единицам статистической совокупности. При этом значения статистического признака у отдельных единиц могут колебаться относительно средней величины под влиянием различных факторов. Например, доходы студентов дневного обучения в целом определяются установленным уровнем государственной стипендии. Очевидно, что средняя величина доходов будет близка к этому уровню. Однако возможны колебания доходов у каждого конкретного студента, поскольку он может работать в свободное от учебы время и получать при этом дополнительный доход, а может вообще не иметь дохода или иметь меньший доход по причине низкой успеваемости в учебе (известно, что наличие государственной стипендии зависит от уровня успеваемости студента).

При осреднении значений количественного признака необходимо учитывать требование качественной однородности статистических единиц – носителей этого признака. В противно случае средняя величина не будет обладать указанным выше свойством и будет являться формальным показателем, не имеющим практического применения. Так, например, не имеет смысла рассчитывать средние доходы работающего населения региона, поскольку население как массовое явление очень неоднородно. В этом случае вначале необходимо разбить население на качественно однородные группы, например, по профессиональному признаку, а затем рассчитать средние доходы в пределах каждой группы.

Наиболее распространенным видом средних величин является средняя арифметическая. Если единицы статистической совокупности не сгруппированы по величине признака, значения которого осредняют, то рассчитывают среднюю арифметическую простую:

,

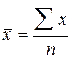где:

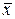- среднее значение признака;

x - значения признака у отдельных единиц;

n – число единиц в совокупности.

Пример 6.3. Рассчитаем на основе данных, представленных в таблице 6.1, среднее значение числа занятых на предприятии.

Решение.

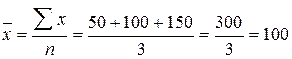чел.

Если значения статистического признака сгруппированы по вариантам, то для их осреднения используют формулу средней арифметической взвешенной:

,

где:

x – варианты значения признака (дискретные значения или середины интервалов);

f – соответствующие вариантам частоты.

Пример 6.4. В таблице 6.2 представлены данные о распределении рабочих производственного кооператива по величине ежемесячной заработной платы. Рассчитаем среднее значение этого признака.

Таблица 6.2

Решение.

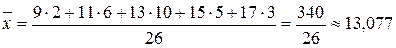тыс. руб.

Если частоты вариантов признака неизвестны, но известны значения произведения вариантов и частот (w= xf), то для осреднения используют формулу средней гармонической взвешенной:

.

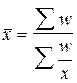Пример 6.5. Дневная выручка трёх магазинов в части продажи сахарного песка составила 1000, 1122 и 1512 руб. при цене за один килограмм 20, 22 и 21 руб. соответственно. Рассчитаем среднее значение цены одного килограмма сахарного песка.

Решение.

Обозначим: x – цена сахарного песка (руб./кг); f – объём продажи сахарного песка (кг); xf = w – выручка от продажи (руб.).

Учитывая характер исходных данных, рассчитаем среднее значение цены одного килограмма сахара по формуле средней гармонической взвешенной:

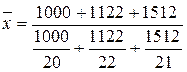≈ 21,01 руб.

Если для всех вариантов осредняемого признака величина w одинакова, то при осреднении используют формулу средней гармонической простой:

.

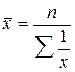Пример 6.6. Согласно технической характеристики три автомобиля имеют бензобаки одинакового объема и разный расход бензина на единицу пути. Двигатель первого автомобиля расходует 6 литров бензина на 100 км, второго – 8 литров, третьего – 9 литров. Определим средний расход бензина на 100 км пути этих автомобилей при наличии одной полной заправки их бензобаков.

Решение.

Обозначим: x – расход автомобилем бензина на 100 км пути; f – путь, пройденный автомобилем на одной заправке бензобака.

Тогда xf = w – объем бензобака автомобиля (постоянный для всех автомобилей).

Учитывая характер исходных данных, средний расход бензина на 100 км пути в пределах одной заправки рассчитаем по формуле средней гармонической простой:

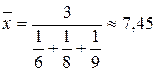литр/100 км.

Необходимо отметить, что все рассмотренные формулы средних величин могут быть использованы для осреднения абсолютных статистических показателей таким же образом, как и для осреднения статистических признаков.

Способ осреднения относительных показателей зависит от их вида. На практике осреднение применяют только для относительных показателей динамики и интенсивности.

Для осреднения относительных показателей динамики рассчитывают среднюю геометрическую простую (для несгруппированных значений показателя) или взвешенную (для сгруппированных значений):

;

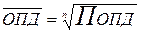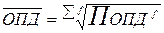
где:

ОПД – отдельные значения (варианты значений) относительного показателя динамики;

f – частоты, соответствующие вариантам.

n – общее число значений относительного показателя динамики.

Пример 6.7. Стоимость основных фондов предприятия на начало каждого квартала отчётного года и первого квартала следующего года составила 1,25; 1,27; 1,26; 1,32; 1,35 млн. руб. соответственно. Рассчитаем среднее значение относительного показателя ежеквартальной динамики стоимости основных фондов.

Решение.

Вначале рассчитаем значения относительного показателя динамики стоимости основных фондов для каждого квартала отдельно:

ОПД₁ = 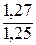= 1,016 (101,6%);

ОПД₂ = 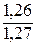≈ 0,992 (99,2%);

ОПД₃= 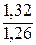≈ 1,048 (104,8%);

ОПД₄ = 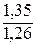≈ 1,071 (107,1%).

Для осреднения этих значений применим формулу средней геометрической простой:

.

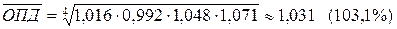Таким образом, в течение года ежеквартально стоимость основных фондов предприятия в среднем возрастала на 3,1%.

Осреднение относительных показателей интенсивности (ОПИ) всегда осуществляется по взвешенным формулам – арифметическим или гармоническим:

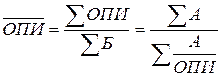, где .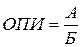

Пример 6.8. Плотность населения трех регионов в составе одного субъекта федеративного государства составляет 10, 12 и 15 тыс. чел./км² при численности населения 2,5; 3,2; 4,5 млн. чел. соответственно (цифры условные). Рассчитаем плотность населения субъекта государства на основе значений этого показателя для отдельных его регионов.

Решение.

Обозначим: А – численность населения; Б – площадь территории, на которой оно проживает. Тогда плотность населения рассчитывается по формуле относительного показателя интенсивности:

.

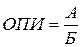Учитывая исходные данные, осредним отдельные варианты плотности населения по формуле средней гармонической взвешенной:

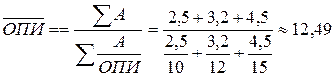тыс. чел./км².

Все рассмотренные в подразделе 6.2 средние показатели относятся к средним степенным. Помимо них к средним статистическим показателям принято относить показатели структуры статистического ряда распределения (см. подраздел 4.2). Однако их величина не зависит от каждого из осредняемых значений, а определяется структурой ряда распределения.

Лекция 4 СТАТИСТИЧЕСКИЙ АНАЛИЗ ВАРИАЦИИ