Вариационного ряда распределения
Для характеристики структуры вариационных рядов распределения рассчитывают структурные показатели – моду и медиану. Мода – это значение признака, наиболее часто встречающееся в ряду, а медиана – значение, делящие ряд распределения на две равновеликие группы.
В дискретном ряду мода равна значению варианта с наибольшей частотой, а медиана – значению первого варианта, для которого накопленная частота превышает половину суммы всех частот. Накопленная частота получается путем суммирования частоты рассматриваемого варианта и частот всех предшествующих вариантов. Например, в ряду распределения квартир по числу комнат (таблица 4.2) чаще всего встречаются 2-комнатные квартиры (40 раз) и, начиная с этого же варианта, накопленная частота (50) превышает половину всех частот (½ ∙ 80 = 40). Последнее означает, что если расположить все восемьдесят квартир дома в порядке возрастания числа комнат, то геометрической серединой этой последовательности будет двухкомнатная квартира, а точнее – две двухкомнатные квартиры.
В интервальном вариационном ряду вначале определяют интервалы, в которых находятся структурные показатели.
При определении модального интервала необходимо учитывать ширину каждого из интервалов. Для этого от частот переходят к плотностям распределения, используя формулу
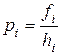 ,
,
где 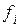 ,
, 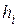 ,
, 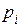 - частота, ширина и плотность распределения единиц в i-ом интервале.
- частота, ширина и плотность распределения единиц в i-ом интервале.
Модальным интервалом является интервал с максимальным значением плотности распределения, а конкретное значение моды внутри него рассчитывается по формуле
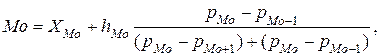
где:
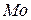 – мода;
– мода;
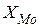 ,
, 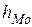 ,
, 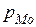 – начало, ширина и плотность распределения модального интервала;
– начало, ширина и плотность распределения модального интервала;
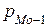 ,
, 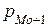 – плотности распределения интервалов, расположенных перед модальным интервалом и после модального интервала.
– плотности распределения интервалов, расположенных перед модальным интервалом и после модального интервала.
При равных по ширине интервалах переходить от частоты к плотности распределения не имеет смысла, поскольку соотношение значений плотности распределения останется таким же, как и соотношение значений частоты. В этом случае следует ориентироваться на максимальное значение частоты и, рассчитывая величину моды, использовать в ее формуле вместо значений плотности распределения соответствующие значения частоты.
Определение медианного интервала не зависит от равенства или неравенства интервалов. В этом случае используют тот же критерий, что и для дискретного ряда, используя только показатель накопленной частоты. Конкретное значение моды внутри этого интервала рассчитывают по формуле
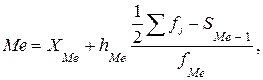
где:
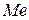 – медиана;
– медиана;
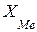 ,
, 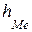 ,
, 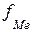 – начало, ширина и частота медианного интервала;
– начало, ширина и частота медианного интервала;
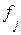 – частота каждого j-го интервала;
– частота каждого j-го интервала;
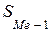 – накопленная частота интервала, расположенного перед медианным интервалом.
– накопленная частота интервала, расположенного перед медианным интервалом.
Пример 4.1. В таблице 4.4 (первая и вторая строки) представлено распределение числа предприятий (ƒ) по числу занятых (чел., х).
Таблица 4.4
| х | До 100 | 100 - 200 | 200 – 300 | 300 – 400 | Итого |
| ƒ | |||||
| S | - |
Рассчитаем значение моды и медианы представленного ряда распределения.
Решение.
Так как 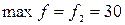 , то модальным является второй интервал.
, то модальным является второй интервал.
Поскольку имеют место равные по ширине интервалы, то
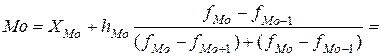
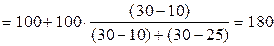 чел.
чел.
Таким образом, в исследуемой статистической совокупности предприятий чаще всего встречаются предприятия с числом занятых, примерно равным 180 чел. Термин «примерно» использован в выводе потому, что мода интервального ряда – это абстрактный показатель. Фактически в исследуемой совокупности могут отсутствовать единицы наблюдения с величиной группировочного признака, строго равной рассчитанному значению моды. Однако, чем ближе значения признака к величине моды, тем больше их число.
Заполним третью стоку таблицы 4.4, указав в ней значения наколенного числа занятых S, и рассчитаем его пороговое значение для определения медианного интервала:
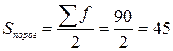 чел.
чел.
Так как 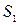 ,
, 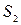 <
< 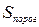 ,
,  >
> 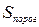 , то медианным интервалом является третий интервал.
, то медианным интервалом является третий интервал.
Тогда
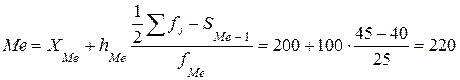 чел.
чел.
Таким образом, число занятых, равное 220 чел., разбивает исследуемую совокупность предприятий на две равновеликие группы. Это означает, что если упорядочить все предприятия по возрастанию числа занятых и поделить на две равные по числу предприятий части, то граница между ними пройдет по числу занятых, примерно равному 220 чел.
Пример 4.2. В таблице 4.5 (первая и вторая строки) представлено распределение числа предприятий (ƒ) по величине балансовой прибыли (тыс. млн., x).
Таблица 4.5
| x | 1 – 2 | 2 – 5 | 5 – 10 | Итого |
| ƒ | ||||
| p | - |
Рассчитаем значение моды представленного ряда распределения.
Решение.
Исследуемый ряд распределения построен на основе неравных интервалов, поэтому перейдем от показателя частоты к плотности распределения и заполним третью строку таблицы 4.5.
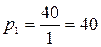 ед./млн. руб.;
ед./млн. руб.;
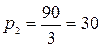 ед./млн. руб.;
ед./млн. руб.;
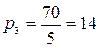 ед./млн. руб.
ед./млн. руб.
Максимальное значение плотности распределения предприятий наблюдается в первом интервале балансовой прибыли, поэтому
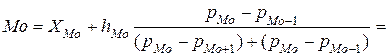
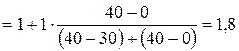 млн. руб.
млн. руб.
Таким образом, несмотря на то, что при проведении статистической группировки больше всего предприятий попало в интервал балансовой прибыли от двух до пяти млн. руб., чаще всего в исследуемой статистической совокупности встречаются предприятия с прибылью, близкой к 1,8 млн. руб.
Дата добавления: 2022-07-20; просмотров: 202;











