ПРЕДСТАВЛЕНИЕ ГРАФОВ
Важным вопросом, особенно для приложений теории графов, является определение возможных способов представления графов. Самый простой способ - полное перечисление множеств V и Е. Однако, очевидно, что в этом случае выявление у графа различных характеристик и свойств будет крайне затруднительным. Граф можно представить в виде некоторого графического изображения и визуально определить некоторые свойства и характеристики заданного графа. Однако, при наличии в графе'большого числа ребер и вершин этот способ также мало пригоден. Рассматривая различные возможные способы представления графов, мы должны иметь в виду потребность ввода соответствующей информации в компьютер. В этой связи ввод информации в числовом виде предпочтителен, хотя современные технические средства допускают ввод и графической информации (таблиц, текста, графиков, рисунков и т.д.), после чего может производиться обработка такой информации.
Матрица смежности. Если вершины графа G помечены метками v1, v2,..., vn, то элементы матрицы смежности A(G) размера V, xV определяются следующим образом: A(i.j) = 1, если vi смежна с vj; A(ij) = 0 в противном случае (рис. 1.9, а).
Матрица инцидентности. Если вершины графа G помечены метками v1, v2,..., vm, а ребра - метками е1, е2,..., еп, то элементыматрицы инцидентности I(G) размера М х N определяются правилом: B(ij) = 1, если vi инцидентна ej; B(iJ) = 0 в противном случае (см. рис. 1.9, б).
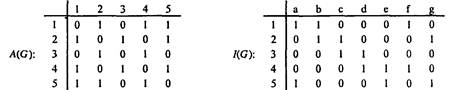
Рис. 1.9, а. Матрица смежности Рис. 1.9, б. Матрица инцидентности
Для ориентированного графа G, имеющего N вершин можно рассмотреть матрицу достижимости C(G) размера N х N, элементы которой определяются так: С(I, J) = 1, если вершина vj достижима из vi; C(I, J) = 0 в противном случае. Ниже приведен пример ориентированного графа и его матрицы достижимости, рис. 1.10.
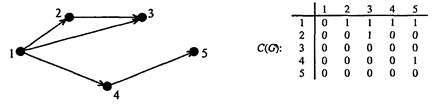
Рис. 1.10. Матрица достижимости ориентированного графа
Контрольные вопросы
1. Каким образом определяется граф?
2. Что является путем в графе?
3. Как определяется такой вид графа, как дерево?
4. Какими способами можно задать граф?
Дата добавления: 2020-02-05; просмотров: 804;











