Метод последовательного исключения переменных по схеме Гаусса.

Численные методы решения систем линейных уравнений

В общем виде систему линейных алгебраических уравнений записывают в виде:

Ax = f,

где А – матрица n xn;

x = (x₁, x₂, …, x_n) – искомый вектор;

f = (f₁, f₂, …, f_n) – заданный вектор.

Предполагается, что определитель Δ ≠ 0, следовательно решение х существует и единственно.

Из курса алгебры известно, что систему линейных алгебраических уравнений можно решить, по крайней мере, двумя способами:

1. по формулам Крамера;

2. методом последовательного исключения неизвестных (методом Гаусса).

Известное из курса высшей алгебры правило Крамера для решения систем линейных алгебраических уравнений (СЛАУ) на практике применяется крайне редко, т.к. требует порядка m!·m арифметических операций для решения системы с m неизвестными.

Используемые практически методы решения СЛАУ можно разделить на две большие группы: так называемые точные методы и методы последовательных приближений (или итерационные).

Точные методы характеризуются тем, что с их помощью принципиально возможно, проделав конечное число операций, получить точные значения неизвестных.

При этом, конечно, предполагается, что коэффициенты и правые части системы известны точно, а все вычисления производятся без округлений.

Но, на практике применение точного метода не гарантирует получения точного решения даже в том случае, когда коэффициенты при переменных и свободные члены уравнений являются точными числами, поскольку в процессе вычислений почти всегда приходится прибегать к округлению чисел. А при наличии иррациональных коэффициентов и свободных членов возникает необходимость замены их рациональными приближениями.

Чаще всего точные методы включают в себя два этапа:

I этап – система преобразуется к тому или иному простому виду (прямой ход);

II этап – решается упрощенная система и находятся значения неизвестных (обратный ход).

Итерационные методы характеризуются тем, что с самого начала задаются какими-то приближенными значениями неизвестных. Из этих приближенных значений тем или иным способом получают новые "улучшенные" приближенные значения. С новыми приближенными значениями поступают точно так же и т.д.

При выполнении определенных условий можно прийти, вообще говоря, после бесконечного числа шагов к точному решению.

Алгоритмы итерационных методов, как правило, очень просты, что объясняет их применимость для решения систем с большим (до 10⁶ и более) числом неизвестных.

Метод Гаусса

Метод последовательного исключения переменных по схеме Гаусса.

Метод Гаусса рассматривается в школьном курсе математики как один из основных методов решения систем линейных уравнений. Существует несколько модификаций этого метода.

Рассмотрим схему единственного деления.

Пусть дана система линейных уравнений:

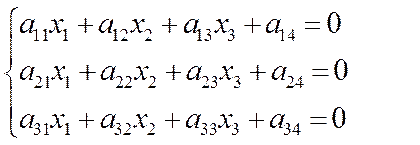(1)

Будем полагать, что а₁₁<>0 (путем перестановки переменных и уравнений всегда можно добиться выполнения этого условия, поскольку определитель ∆≠0, и, следовательно, всегда найдется уравнение, в котором а_ij≠0).

Из первого уравнения системы (1) выразим х₁:

х₁ = α₁₂х₂ + α₁₃х₃ + α₁₄, (2)

где

α_1k =‑ (k = 2, 3, 4).

Подставляя (2) во второе и третье уравнения системы (1), придем к следующей системе уравнений:

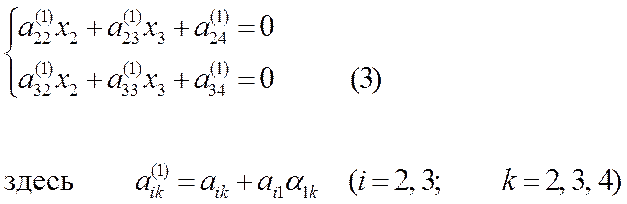
Полагая теперь, что 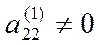, выразим х₂ из первого уравнения системы (3):

х₂= α₂₃х₃ + α₂₄, (4)

где

α_2k =‑ (k = 3, 4).

Подставляя (4) во второе уравнение системы (3), получим:

где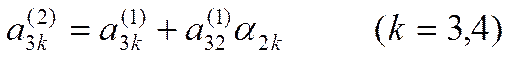

Из (5) определим х₃:

х₃ = α₃₄, (6)

где

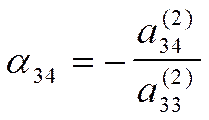
уравнение (6) является итоговым в прямом ходе.

Объединяя уравнения (2), (4) и (6), получим треугольную систему:

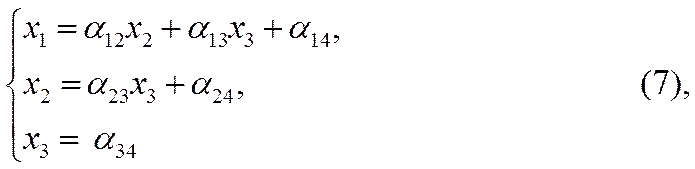
из которой легко найти значения переменных.

Приведение исходной системы (1) к треугольному виду (7) называется прямым ходом; вычисление значений переменных по формулам (7) – обратным.

Контроль вычислений. При решении задач численными методами необходимо уметь осуществлять проверку правильности полученных результатов, т.е. проводить заключительный контроль вычислений. Если объем велик, то желательно проверять и промежуточных результатов, т.е. осуществлять текущий контроль вычислений.

Одной из форм заключительного контроля является непосредственная проверка полученного решения путем подстановки найденных значений неизвестных в исходную систему уравнений (1).

Если все вычисления были точными, то в результате подстановки должны получиться нули.

Если же в процессе вычислений допускались округления, то будут получаться числа d₁, d₂, d₃, отличные от нуля и называемые невязками.

Если невязки достаточно малы, то можно ожидать, что решение получено с малой погрешностью.

В рассмотренной нами схеме числа 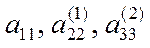играют особую роль (на них делятся коэффициенты уравнений). Они называются ведущими элементами. Если значения ведущих элементов малы, то при вычислениях будут получаться значительные погрешности.