Реляционная алгебра
В основе реляционной модели лежит математическое понятие теоретико-множественного отношения. Теоретико-множественное отношение представляет собой подмножество декартова произведения доменов. Доменом называется набор значений элементов данных одного типа, отвечающий поставленным условиям (например, домен ФИО определяется на базовом типе строк символов, но в число его значений могут входить только те строки, которые могут изображать имя).
Декартовымпроизведениемk доменов (D1, D2,…, Dk), (обозначается D1×D2×…×Dk), называется множество всех кортежей вида (V1, V2, …, Vk) длины k, таких, что V1∈D 1, V2∈D2, …, Vk∈Dk.
Например, пусть D1 = {1, 2, 3}; D2 = {a, b, c, d}
Тогда
| 1,a | 1,b | 1,c | 1,d | в матричном виде | ||
 D1×D2 = D1×D2 =
| 2,a | 2,b | 2,c | 2,d | ||
| 3,a | 3,b | 3,c | 3,d |
или:
D1×D2 = {(1,a), (1,b), (1,c), (1,d), (2,a), (2,b), (2,c), (2,d), (3,a), (3,b), (3,c), (3,d)}
Отношением называют некоторое подмножество декартова произведения доменов (предполагаются только конечные отношения).
Примеры отношений:
1) {(1,a), (1,c), (1,b)} - подмножество декартова произведения доменов D1×D2;
2) Ø.
В реляционных СУБД для выполнения операций над отношениями используют две группы языков, имеющие в качестве своей математической основы теоретические языки запросов, предложенные Э. Коддом:
· реляционную алгебру;
· реляционное исчисление.
Реляционнойалгеброй называют систему операций манипулирования отношениями, каждый оператор которой в качестве операнда имеет одно или более отношений и образует отношение по заранее обусловленному правилу.
Вариант реляционной алгебры, предложенный Коддом, включает в себя следующие операции: объединение, разность, пересечение, декартово (прямое) произведение, выборка (селекция), проекция, деление и соединение. Упрощенное графическое представление перечисленных операций показано на рис. 4.1.
1) Объединением двух отношений (r ∪ s) является отношение, содержащее все кортежи, которые принадлежат либо r, либо s, либо им обоим.
Данная операция применяется к отношениям с одной и той же схемой.
Схемойотношенияr называется конечное множество имен атрибутов {A1, A2, …, An}.
Примеры:
a) Пусть k и m – отношения со схемой ABC:
| k | (A | B | C) | m | (A | B | C) | |
| a1 | b1 | c1 | a1 | b2 | c1 | |||
| a1 | b2 | c1 | a2 | b2 | c1 | |||
| a2 | b1 | c2 | a2 | b2 | c2 |
Тогда объединение данных отношений:
| k ∪ m = | (A | B | C) |
| a1 | b1 | c1 | |
| a1 | b2 | c1 | |
| a2 | b1 | c2 | |
| a2 | b2 | c1 | |
| a2 | b2 | c2 |
б) Пусть отношение R1 – множество поставщиков из Москвы, а R2 – множество поставщиков, которые поставляют деталь D1:
R1 R2
| №_П | ФИО_П | Город_П | №_П | ФИО_П | Город_П | |
| Р1 | Иванов И. И. | Москва | Р1 | Иванов И. И. | Москва | |
| Р4 | Петров П. П. | Москва | Р2 | Сидоров С. С. | Киев |
Тогда объединение данных отношений даст поставщиков из Москвы, либо поставщиков, которые поставляют деталь D1, либо тех и других:
R1 ∪ R2
| №_П | ФИО_П | Город_П |
| Р1 | Иванов И. И. | Москва |
| Р4 | Петров П. П. | Москва |
| Р2 | Сидоров С.С. | Киев |
2) Разностью двух отношений (обозначается r - s) является отношение, содержащее все кортежи, которые принадлежат r, но не принадлежат s.
Операция применяется к отношениям с одной и той же схемой.
Примеры:
а)
| k – m = | (A | B | C) |
| a1 | b1 | c1 | |
| a2 | b1 | c2 |
б) Разность отношений R1 и R2 даст поставщиков из Москвы, не поставляющих деталь D1:
R1 – R2
| №_П | ФИО_П | Город_П |
| Р4 | Петров П. П. | Москва |
3) Пересечением двух отношений (обозначается r ∩ s) является отношение, содержащее все кортежи, которые принадлежат одновременно r и s.
Операция применяется к отношениям с одной и той же схемой.
Примеры.
а)
| k ∩ m = | (A | B | C) |
| a1 | b2 | c1 |
б) Пересечение отношений R1 и R2 даст всех поставщиков из Москвы, поставляющих деталь D1:
R1 ∩ R2
| №_П | ФИО_П | Город_П |
| Р1 | Иванов И. И. | Москва |


Рис. 4.1. Основные операции реляционной алгебры
4) Декартовымпроизведением отношения r степени k1 и отношения s степени k2 (r × s) является отношение степени (k1 + k2), содержащее такие кортежи, первые k1 элементов которых принадлежат r, а последние k2 элементов принадлежат s.
Примеры:
а) Даны отношения k и m
| k | (A | B) | m | (C | D) | |
| a1 | b1 | c1 | d1 | |||
| a2 | b1 | c2 | d1 | |||
| c2 | d2 |
Тогда
| k × s = | (A | B | C | D) |
| a1 | b1 | c1 | d1 | |
| a1 | b1 | c2 | d1 | |
| a1 | b1 | c2 | d2 | |
| a2 | b1 | c1 | d1 | |
| a2 | b1 | c2 | d1 | |
| a2 | b1 | c2 | d2 |
б) Пусть отношение R1 – множество поставщиков, а S1 – множество деталей:
R1 S1
| №_П | ФИО_П | Город_П | №_Д | Название | Вес | Город_Д | |
| Р1 | Иванов И. И. | Москва | Д1 | гайка | Москва | ||
| Р2 | Сидоров С. С. | Киев | Д3 | винт | Ростов | ||
| Д6 | шпилька | Москва |
Тогда декартово произведение данных отношений:
R1 × S1
| №_П | ФИО_П | Город_П | №_Д | Название | Вес | Город_Д |
| Р1 | Иванов И.И. | Москва | Д1 | гайка | Москва | |
| Р1 | Иванов И.И. | Москва | Д3 | винт | Ростов | |
| Р1 | Иванов И.И. | Москва | Д6 | шпилька | Москва | |
| Р2 | Сидоров С.С. | Киев | Д1 | гайка | Москва | |
| Р2 | Сидоров С.С. | Киев | Д3 | винт | Ростов | |
| Р2 | Сидоров С.С. | Киев | Д6 | шпилька | Москва |
5) Выборка (применяется к одному отношению). Результатом ее применения к отношению r является другое отношение, представляющее собой подмножество кортежей отношения r с определенным значением в выделенном атрибуте.
Пусть r отношение со схемой R, A – атрибут в R и a – элемент из домена А. Тогда 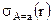 – операция выборки в r кортежей, в которых значение A равно a. В условии выборки можно использовать константы, логические операции и операции сравнения.
– операция выборки в r кортежей, в которых значение A равно a. В условии выборки можно использовать константы, логические операции и операции сравнения.
Примеры:
а)
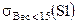
| №_Д | Название | Вес | Город_Д |
| Д1 | гайка | Москва |
б) Дано отношение R1
R1
| №_П | №_Д | Количество |
| Р1 | Д1 | |
| Р1 | Д3 | |
| Р2 | Д1 | |
| Р2 | Д4 | |
| Р3 | Д1 |
Тогда
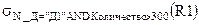
| №_П | №_Д | Количество |
| Р3 | Д1 |
6) Проекция(применяется к одному отношению) - операция выбора подмножества столбцов. Пусть r – отношение со схемой R, Х – подмножество из R. Проекция r на X 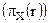 есть отношение
есть отношение 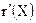 , полученное вычеркиванием столбцов, соответствующих атрибутам в R – X, и исключением из оставшихся столбцов повторяющихся строк.
, полученное вычеркиванием столбцов, соответствующих атрибутам в R – X, и исключением из оставшихся столбцов повторяющихся строк.
Примеры.
а) Пусть k - отношение со схемой АВС:
| k | (A | B | C) |
| a1 | b1 | c1 | |
| a1 | b2 | c1 | |
| a2 | b1 | c2 |
Тогда запись 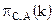 означает, что из каждого кортежа, принадлежащего k, формируется кортеж длины 2 из третьего и первого его атрибутов в указанном порядке:
означает, что из каждого кортежа, принадлежащего k, формируется кортеж длины 2 из третьего и первого его атрибутов в указанном порядке:
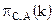 = =
| (C | A) | повторяющиеся кортежи исключаются | |
| c1 | a1 | |||
| c2 | a2 |
Записи 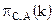 эквивалентна запись
эквивалентна запись 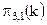 .
.
б) Пусть S1 - отношение, содержащее информацию о деталях:
S1
| №_Д | Название | Вес | Город_Д |
| Д1 | гайка | Москва | |
| Д3 | винт | Ростов | |
| Д6 | шпилька | Москва |
Тогда
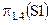
| №_Д | Город_Д |
| Д1 | Москва |
| Д3 | Ростов |
| Д6 | Москва |
7) Деление. Пусть r – отношение со схемой R, s – отношение со схемой S и S ⊆ R. Положим 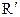 = R – S. Частное от деления r на s (r ÷ s) – это максимальное подмножество
= R – S. Частное от деления r на s (r ÷ s) – это максимальное подмножество 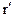 множества
множества 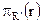 , такое, что декартово произведение
, такое, что декартово произведение 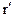 и s содержится в r.
и s содержится в r.
Примеры:
а) Даны отношения k и m
| k | (A | B | C | D) | m | (C | D) | |
| a1 | b1 | c1 | d2 | c2 | d1 | |||
| a2 | b2 | c2 | d1 | c4 | d1 | |||
| a3 | b2 | c3 | d3 | |||||
| a2 | b2 | c4 | d1 | |||||
| a1 | b3 | c5 | d4 | |||||
| a4 | b1 | c6 | d5 |
Тогда
| k ÷ m = | (A | B) |
| a2 | b2 |
б) Имеется отношение
Право
| Пилот | Тип_самолета |
| Иванов | |
| Иванов | |
| Иванов | |
| Петров | |
| Петров | |
| Сидоров | |
| Сидоров | |
| Сидоров | |
| Сидоров | |
| Макаров |
Требуется найти тех пилотов, которые имеют право управлять всеми типами самолета из некоторого множества q.
q
| Тип_самолета |
Тогда
Право ÷ q
| Пилот |
| Иванов |
| Сидоров |
8) Соединение.
Естественноесоединение. Пусть r – отношение со схемой R, s – отношение со схемой S и R ∪ S = T. Естественным соединением отношений r и s (r ⊲⊳ s) является отношение q со схемой T, содержащее кортежи, каждый являющийся комбинацией кортежа из r и кортежа из s с равными (R ∩ S) – значениями.
Примечание. Если R ∩ S = ∅, то r ⊲⊳ s даст декартово произведение r и s.
Примеры:
а) Даны отношения k и m
| k | (A | B) | m | (B | C) | |
| a1 | b1 | b1 | c2 | |||
| а1 | b2 | b2 | c1 | |||
| a2 | b1 |
Тогда
| k ⊲⊳m = | (A | B | C) |
| a1 | b1 | c2 | |
| a2 | b1 | c2 | |
| a1 | b2 | c1 |
б) Даны отношения R1 и S1
R1 S1
| №_П | ФИО_П | Город_П | №_Д | Название | Вес | Город_Д | |
| Р1 | Иванов И. И. | Москва | Д1 | гайка | Москва | ||
| Р2 | Сидоров С. С. | Киев | Д3 | винт | Ростов | ||
| Д6 | шпилька | Москва |
Естественное соединение R1 и S1 по атрибуту Город (в отношении R1 – это Город_П, а в отношении S1 – Город_Д):
R1 ⊲⊳ S1
| №_П | ФИО_П | Город | №_Д | Название | Вес |
| Р1 | Иванов И.И. | Москва | Д1 | гайка | |
| Р1 | Иванов И.И. | Москва | Д6 | шпилька |
Тета – соединение. При естественном соединении отношения могут комбинироваться только по одноименным столбцам и должны комбинироваться по всем таким столбцам.
Примечание. В предыдущем примере вначале была применена операция переименования атрибутов Город_Д и Город_П на Город.
Отношения могут соединяться также по столбцам с различными именами атрибутов, но равными доменами.
Тета – соединение отношений r и s по столбцам i и j 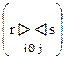 представляет собой множество кортежей в декартовом произведении r и s, таких, что i-й элемент r находится в связи Θ с j–элементом s.
представляет собой множество кортежей в декартовом произведении r и s, таких, что i-й элемент r находится в связи Θ с j–элементом s.
Если Θ является оператором «=», то эта операция называется эквисоединением.
Примеры
а) Пусть R1 – отношение, содержащее информацию о рейсах из города «а» в город «в», S1 – отношение, содержащее информацию о рейсах из города «в» в город «с»:
R1
| Номер | Время_вылета | Время_прибытия |
| 9.40 | 11.45 | |
| 12.50 | 14.47 | |
| 16.05 | 18.15 | |
| 20.30 | 22.25 | |
| 21.15 | 23.11 |
S1
| Номер | Время_вылета | Время_прибытия |
| 8.30 | 9.52 | |
| 12.25 | 13.43 | |
| 16.20 | 17.40 | |
| 19.10 | 20.35 |
Требуется узнать, какие рейсы из «a» в «в» сочетаются с рейсами из «в» в «c».
Для этого необходимо соединить те кортежи, для которых Время_прибытия в отношении R1 меньше Время_вылета в отношении S1.
Тета – соединение отношений R1 и S1:
| Номер | Время_вылета | Время_прибытия | Номер | Время_вылета | Время_прибытия |
| 9.40 | 11.45 | 12.25 | 13.43 | ||
| 9.40 | 11.45 | 16.20 | 17.40 | ||
| 9.40 | 11.45 | 19.10 | 20.35 | ||
| 12.50 | 14.47 | 16.20 | 17.40 | ||
| 12.50 | 14.47 | 19.10 | 20.35 | ||
| 16.05 | 18.15 | 19.10 | 20.35 |
б) Даны отношения Маршрут и Адрес
Маршрут
| Номер | Пункт_отправления | Пункт_назначения |
| Чикаго | Нью-Йорк | |
| Нью-Йорк | Лос-Анджелес | |
| Атланта | Бостон | |
| Нью-Йорк | Бостон | |
| Бостон | Нью-Йорк |
Адрес
| Пилот | Аэропорт | отношение указывает для каждого пилота адрес базового аэропорта, к которому он приписан | |
| Терхьюн | Нью-Йорк | ||
| Темпл | Атланта | ||
 Тейлор Тейлор
| Атланта | ||
| Тарбелл | Бостон | ||
| Тодд | Лос-Анджелес | ||
| Трумен | Чикаго |
Требуется назначить пилотов на те рейсы, пункт отправления которых совпадает с аэропортом, к которому приписан пилот.
Эквисоединение отношений Маршрут и Адрес по столбцам Пункт_отправления и Аэропорт:
| Номер | Пункт_отправления | Пункт_назначения | Пилот | Аэропорт |
| Чикаго | Нью-Йорк | Трумен | Чикаго | |
| Нью-Йорк | Лос-Анджелес | Терхьюн | Нью-Йорк | |
| Атланта | Бостон | Темпл | Атланта | |
| Атланта | Бостон | Тейлор | Атланта | |
| Нью-Йорк | Бостон | Терхьюн | Нью-Йорк | |
| Бостон | Нью-Йорк | Тарбелл | Бостон |
Основное отличие эквисоединения от естественного в том, что при последнем соединяемые столбцы не повторяются.
По справедливому замечанию Дейта, реляционная алгебра Кодда обладает несколькими недостатками. Во-первых, восемь перечисленных операций по охвату своих функций, с одной стороны, избыточны, так как минимально необходимый набор составляют пять операций: объединение, вычитание, произведение, проекция и выборка. Три другие операции (пересечение, соединение и деление) можно определить через пять минимально необходимых. Во-вторых, этих восьми операций недостаточно для построения реальной СУБД на принципах реляционной алгебры. Требуются расширения, включающие операции: переименования атрибутов, образования новых вычисляемых атрибутов, вычисления итоговых функций, построения сложных алгебраических выражений, присвоения, сравнения и т. д.
Дата добавления: 2016-06-15; просмотров: 3606;











