Квантовая теория теплопроводности твердых тел

(по Эйнштейну)

Эйнштейн, учитывая недостатки классической теории, предположил:

1.Как и в классической теории, твердое тело – это совокупность N независимых атомов, колеблющихся с одинаковой частотой ;

2.Однако средняя энергия, приходящаяся на одну степень свободы равна не кТ, а вычисляется по формуле Планка:

;

3.Энергия одного моля вещества, имеющего 3 степени свободы:

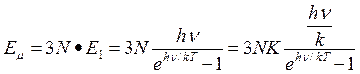
где = 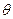- характеристическая t⁰ тела.

Тогда:

4.Атомная теплоемкость твердого тела:

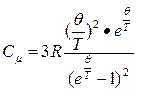(2)

Преимущества этой формулы перед классической ( ):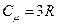

а) при низких t⁰ (Т << 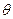), 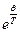>> 1 Поэтому единицей в знаменателе можно пренебречь, и тогда:

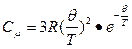
б) при Т 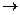0, а . Тогда:

Т.е. подтверждает экспериментальную зависимость в области низких температур.

в) при высоких температурах формула (2) переходит в формулу (1).

Таким образом, теория теплоемкости Эйнштейна качественно согласуется с опытом. Однако количественно эта теория расходится с опытом, особенно в области низких температур. Причина расхождения – грубое предположение, что все атомы твердого тела колеблются с одинаковой частотой.

Теория Дебая

1.Система, состоящая из N атомов, обладает 3N степенями свободы.

2.В системе возникает 3N колебаний, совершающихся с различными (собственными) частотами.

3.Число собственных колебаний твердого тела (z), имеющие частоты, меньше :

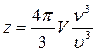
где V – объем тела

- скорость распространения колебаний в твердом теле.

4.max число собственных колебаний

5.max частота этих колебаний

;

где 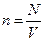- число атомов в единице объема

6.Число собственных колебаний тела dz, приходящееся на интервал частот от до :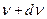

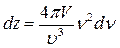
7.Энергия dz колебаний, имеющих частоты в интервале от до :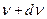

8.Энергия всего твердого тела:

где: ; - характеристическая температура Дебая

9.Атомная плотность твердого тела:

(3) – формула Дебая

Преимущества формулы Дебая:

а) При высоких температурах (Т >> )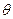

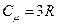т.е. приводит к закону Дюлонга и Пти.

б) Для низких температур (Т << )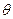

где для каждого твердого тела.

Т.е. в области низких температур формула Дебая приводит к кубической зависимости теплоемкости от температуры, что полностью соответствует опытным данным.