Алгебраический метод

Алгебраический метод предполагает построение некоторого отрезка по формуле. Такие построения входят в таблицу основных построений.

14.

Построение отрезка, четвёртого пропорционального к трём данным отрезкам.

А, с. 163, № 628; П, с. 78, задача 6.1

Даны отрезки a, b и c.

Дано:

Построить отрезок .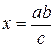

План построения:

1) угол АВС;

2) от вершины В на ВА отложить отрезок BD = а;

3) от вершины В на ВС отложить последовательно отрезки BL = с и LK = b.

4) DL.

5) МК || DL.

6. DM = x

15.

Построение отрезка, среднего пропорционального к двум данным отрезкам.

П, с. 95, № 15. Даны отрезки a и b. Как простроить отрезок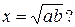

Дано: Построение:

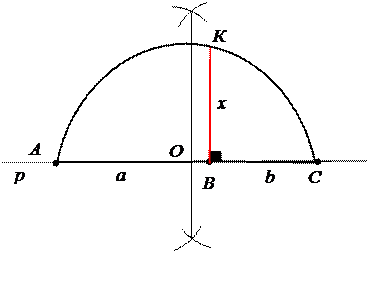
Построить отрезок: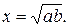

Построение.

1. Прямая р. 2. АВ = а. 3. ВС = b. 4. О – середина АС. 5. Окр. (О; ОА).

6. ВК ^ АС. 7. ВК = х.

Отметим, что в учебнике П. в связи с изучением теоремы Пифагора учащимся предлагается построить отрезки по формулам 1) 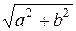; 2) 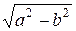.(С. 95)

В учебнике А. этот метод в явном виде не рассматривается. Однако, в дополнительных задачах к главе VII предлагается задача № 627 (с. 163). Дан треугольник АВС. Постройте DA₁B₁C₁, подобный DАВС, площадь которого в 2 раза больше площади треугольника АВС.

Анализ. Так как площадь DA₁B₁C₁ в 2 раза больше площади DАВС и эти треугольники подобны, то стороны DA₁B₁C₁ в 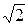раз больше сторон DАВС.

То есть, если ВС= а, то B₁C₁= 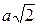. Отрезок, заданный такой формулой, есть диагональ квадрата со стороной а. Отсюда ясно построение DA₁B₁C₁.

Таким образом, геометрические задачи на построение являются ценным дидактическим материалом, способствующим формированию умений работать с чертёжными инструментами, усвоению теоретических основ курса, развитию логического мышления, алгоритмической культуры учащихся.