Метод геометрических мест точек

Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определённым свойством (П. с. 61).

Основные ГМТшкольного курса планиметрии:

1. Окружность: гмт плоскости, обладающих свойством равноудалённости от данной точки (П., с.61).

2. Биссектриса неразвёрнутого угла: гмт плоскости, равноудалённых от сторон угла (А. с. 176).

3. Серединный перпендикуляр к отрезку: гмт плоскости, равноудалённых от концов отрезка (А., с.177, П. с. 61).

4. Две прямые, параллельные данной и отстоящие от неё на h: гмт плоскости, удалённых от данной прямой на данное расстояние.

Сущность метода: задачу сводят к нахождению точки обладающей двумя свойствами, вытекающими из требования задачи.

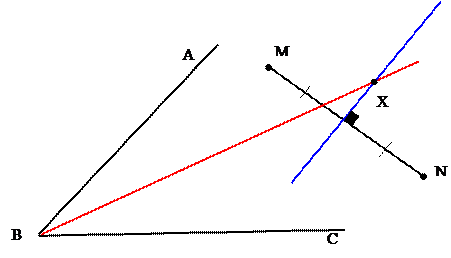
Задача № 688 (А. с. 181). Даны угол и отрезок. Постройте точку, лежащую внутри данного угла, равноудалённую от его сторон и равноудалённую от концов данного отрезка.

Рассмотрим задачу № 39 из учебника Погорелова (с. 65): постройте треугольник по стороне и проведённым к ней медиане и высоте.

Анализ. План построения.

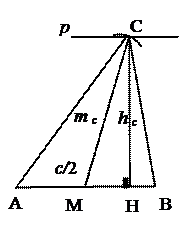
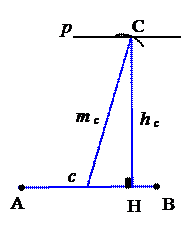
1. АВ.

2. М – середина АВ.

3. Окр. (М, т_с).

4. Прямая р, параллельная АВ

и отстоящая от неё на h_c.

5. C.

6. DABC – искомый.

Приведём примеры задач, решаемых методом геометрических мест точек (методом пересечений) из учебников.

Атанасян: 293, 294, 357, 687, 736, 737.

Погорелов: п. 49, № 43; № 44; № 45,№ 45; № 48, п. 107 № 53.

Метод подобия

Суть метода состоит в том, что на основании некоторых данных строят фигуру, подобную искомой, а затем, используя остальные данные, строят искомую фигуру.

Задача 3 (А., с. 149, объяснительный текст учебника).

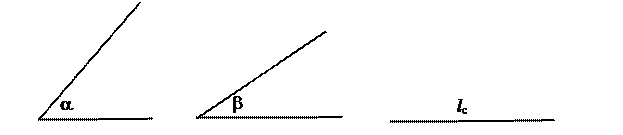Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.

Дано.

Построить DABC.

Условия: ÐА=a, ÐВ=b, CL – биссектриса ÐС, CL= l_с.

Анализ.

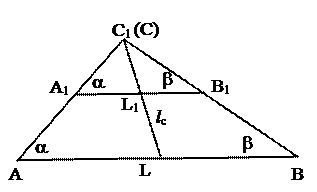Исключим из условия биссектрису угла С и построим DA₁B₁C₁ с углами, равными a и b, подобный искомому. Построим его биссектрису C₁L₁ и отложим на ней отрезок CL, равный l_с. Остаётся через точку L провести прямую, параллельную АВ. Полученный треугольник АВС – искомый.

Задача 9 (П., п.102, с.156).

Впишите в данный треугольник квадрат, у которого две вершины лежат на одной стороне, две другие вершины – на двух других сторонах.

Анализ.

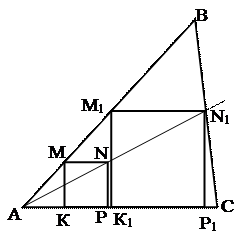
Рассмотрим квадрат, у которого три вершины лежат на сторонах треугольника. Такой квадрат определяется неоднозначно и может быть построен. КМNP – один из таких квадратов. Искомый квадрат подобен (гомотетичен) построенному. Его вершина N₁

лежит на луче AN и стороне треугольника ВС.

План построения.

1. Квадрат KMNP. 2. Луч AN 3. N₁ = AN ∩ ВС. 4. Квадрат К₁М₁N₁Р₁.

Приведём примеры задач, решаемых методом подобия из учебников.

Атанасян: 587 - 590, 629

Погорелов: п.102, № 8.