Параллельные прямые в курсе геометрии 7 класса
Основная цель: сформировать понятие параллельных прямых.
Выше была приведена схема формирования понятия по 5 позициям: определение, символическое обозначение, геометрическая интерпретация, свойства и признаки, приложения. Формирование понятия параллельных прямых идеально укладывается в эту схему.
Содержание учебного материала
Содержание учебного материала описывается посредством блок схемы.
Блок схема состоит из 3 блоков А, В, С.
Блок А – ранее изученный материал, используемый в данной теме.
Блок В – теоретический материал данной темы, который делится на 3 блока:
В1 - основные понятия и предложения темы;
В2 – сопутствующий материал;
В3 – вырабатываемый в этой теме аппарат, применяемый в других темах и при решении задач;
С – приложения данной темы.
Блок – схемы представляются в следующем виде:

Рис. 1Анализ учебного материала позволяет составить следующую блок –
схему темы «Параллельные прямые»
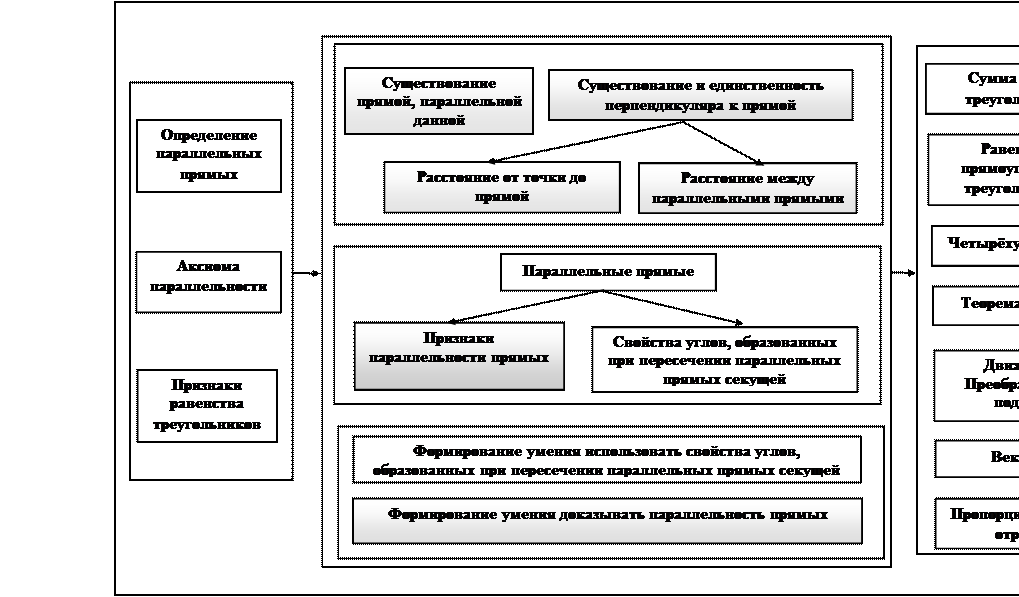 Блок – схема темы «Параллельные прямые» по учебнику А.В. Погорелова
Блок – схема темы «Параллельные прямые» по учебнику А.В. Погорелова
Проведём сравнительный анализ учебного материала
| Учебник А.В. Погорелова | Учебник Л.С. Атанасяна | |
| Определение Две прямые на плоскости называются параллельными, если они не пересекаются (А). Две прямые называются параллельными, если они не пересекаются (П). | ||
| Терминология | ||
| Углы: внутренние односторонние; внутренние накрест лежащие; соответственные. | Углы: накрест лежащие; односторонние; соответственные. | |
| Признаки параллельности прямых | ||
| 1)Две прямые, параллельные третьей, параллельны. 2), 3) Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны. 4) Две прямые, перпендикулярные третьей, параллельны между собой. 5) Прямые параллельны, если соответственные углы равны. | 1) Две прямые, перпендикулярные к третьей не пересекаются. Если при пересечении двух прямых секущей 2) внутренние накрест лежащие углы равны; 3) соответственные углы равны; 4) сумма односторонних углов равна 180°, то прямые параллельны. 5 Если две прямые параллельны третьей прямой, то они параллельны. | |
| Свойства углов, образованных двумя параллельными прямыми и секущей | ||
| Если две параллельные прямые пересечены третьей прямой, то 1)внутренние накрест лежащие углы равны; 2) сумма внутренних односторонних равна 180°. | Если две параллельные прямые пересечены секущей, то 1) накрест лежащие углы равны; 2) соответственные углы равны; 3) сумма односторонних углов равна 180°. | |
Заглянем «внутрь».
1. В учебнике П. сложно вводятся углы, образованные при пересечении двух прямых секущей.
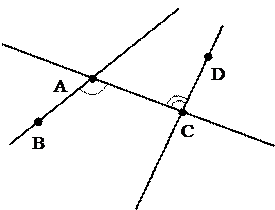
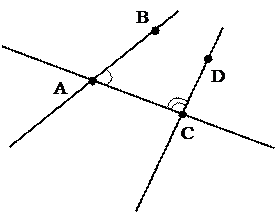
Рис. 2 Рис. 3
2. Доказывается, что
· если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны;
· если внутренние накрест лежащие углы равны, то сумма внутренних односторонних углов равна 180° и обратно: если сумма внутренних односторонних углов равна 180, то внутренние накрест лежащие углы равны.
Потому признак параллельности в учебнике П. может быть записан в виде «Если . . . . . . . . . ,то прямые параллельны», где вместо пропуска может быть вписано любое из условий:
внутренние накрест лежащие углы равны;
сумма внутренних односторонних углов равна 180°.
В учебнике А. всё доступнее.
Рассмотрим доказательства признака параллельности прямых по равенству накрест лежащих углов.
П. Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180 °, то прямые параллельны.
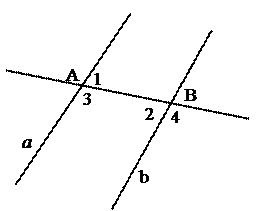 Дано: Дано: a , b – прямые.
Дано: Дано: a , b – прямые.
АВ – секущая.
Ð1=Ð2, Ð3=Ð4.
Доказать: a || b
Рис. 4
Пусть прямые a и b не параллельны и пересекаются в точке С.
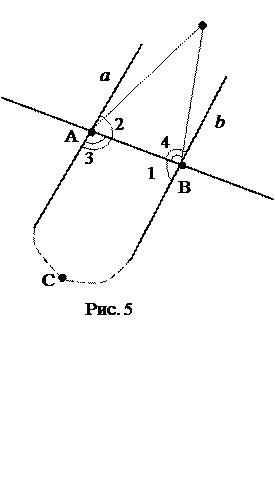
|
1. Построим DВАС1 = DАВС, причём точки С и С1 лежат в разных полуплоскостях относительно прямой АВ.
Тогда Ð1=ÐСВА=ÐВАС1 (по определению равных треугольников).
Ð1 =Ð2 (по условию).
Вывод: Ð2==ÐВАС1, следовательно,
АС1 и а совпадут.
2) Аналогично,
Ð3=ÐСАВ=ÐС1ВА,
Ð3=Ð 4.
Вывод: ÐС1ВА=Ð 4.
АС1 и а совпадут.
Получили две различные прямые, проходящие через точки А и В. Противоречие аксиоме 1.
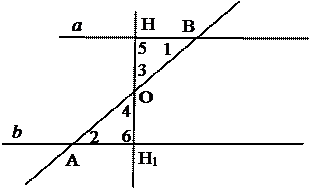
|
АВ – секущая.
Ð1=Ð2.
Доказать: a || b
Д.П. 1. АО=ОВ. 2. ОН ^а.
4. АН1=НВ. 5. Н1О.
Рис.6
Доказательство
1. DОНВ=DОН1А ( 1 признак).
2. Ð3=Ð4: точки Н, О, Н1 – лежат на одной прямой.
3. Ð5=Ð6, Ð5=90°: Ð6=90°.
Вывод: a || b
Приложения этого материала рассмотрим на примере теоремы о сумме углов треугольника.

Доказательство

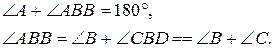
Следовательно, ÐА+ÐВ+ÐС=180°.
Рис. 7
|
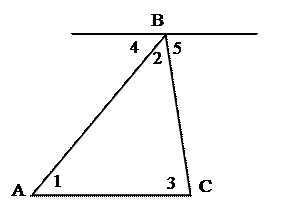
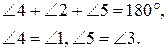
Следовательно, Ð1+Ð2+Ð3=180°.
Рис. 8
| <== предыдущая лекция | | | следующая лекция ==> |
| Основной закон теплопроводности | | | Наличный и безналичный денежный оборот |
Дата добавления: 2016-06-15; просмотров: 3740;











