Электропроводность твердых диэлектриков в сильных полях

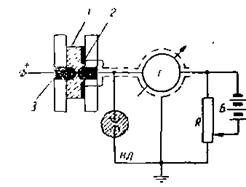Рис. 5‑15 Схема для исследования зависимости / (U) в кристаллах (по Г.А. Воробьеву, В.А. Кострыгину и Н.П. Кострыгиной). 1 — образец; 2 — охранный электрод; 3 — высоковольтный электрод.

Твердый диэлектрик согласно представлениям, выдвинутым Я.И. Френкелем, по своим электрическим свойствам близок к сжатому газу. Это, в частности, подтверждается тем, что электрическая прочность сильно сжатых газов близка к прочности кристаллов. Так, электрическая прочность азота при давлении 100 am достигает 1000 кв/см.

Поэтому следует допустить, что в твердых диэлектриках при воздействии сильных полей возможно развитие ударной ионизации.

Выяснению характера электропроводности были посвящены исследования диэлектриков в тонких слоях.

В твердых диэлектриках толщиной 10^-3—10^-4 см наблюдается увеличение электрической прочности E_пр с уменьшением толщины. При этом E_пр > Е₀ , где Е₀ — напряженность поля в твердом диэлектрике, при которой начинается ударная ионизация. Следовательно, если взять твердый диэлектрик малой толщины и приложить к нему такое напряжение U, чтобы 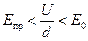, то должны наблюдаться токи ударной ионизации.

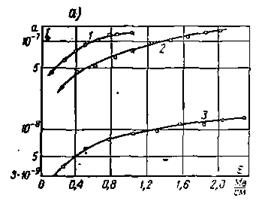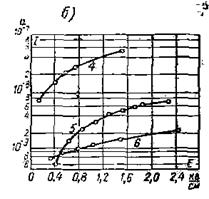Рис. 5‑16 Зависимости тока от напряженности поля для кристаллов: а — КС1; б — NaCI. Расстояния между электродами: 1 — 18,4 мк; 2 — 11,5 мк; 3 — 9,2 мк; 4 — 16,1 мк; 5 — 9,2 мк; б — 6,9 мк

Такие опыты на постоянном напряжении с кристаллами NaCI и КС1 были проведены по схеме, представленной на Рис. 5‑15. В качестве электрода при исследовании кристаллов NaCI был применен раствор NaCI, а при исследовании кристаллов КС1 — раствор КСl. Ток, идущий через образец, измерялся гальванометром Г. Помимо этого тока, через гальванометр должен был протекать ток, вызванный возникающей в электролите э. д. с.; для компенсации этого тока включались батарея Б с потенциометром R. Для защиты гальванометра в случае пробоя образца была применена неоновая лампа НЛ.

Измерения начинались с образцов с наибольшей толщиной d,необходимых для опытов ( 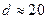мк) и исследовалась зависимость I(U). Затем толщина образца уменьшалась и вновь исследовалась зависимость I(U). Так на одном образце удавалось исследовать зависимость I(U) для трех-четырех межэлектродных расстояний. При такой методике исследования удалось избежать разброса значений тока для различных образцов.

На Рис. 5‑16 представлены зависимости i(E) для кристаллов NaCI и КС1 при различных d.

По графикам Рис. 5‑16 построена зависимость I == f(d) при Е = const (Рис. 5‑17).

С увеличением межэлектродного расстояния ток возрастает, как это и следует из теории ударной ионизации. Однако предсказываемая теорией линейная зависимость логарифма тока I от расстояния здесь не выполняется. Причиной этого расхождения является, по-видимому, влияние объемного заряда, обусловленного высоковольтной поляризацией и захватом электронов у катода; этот заряд искажает поле в диэлектрике.

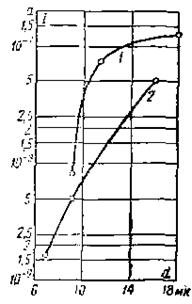Рис. 5‑17 Зависимость тока от толщины кристалла в сильном поле. 1— КС1 при E= I MВ/см; 2 — NaCI при Е = 1,5 MВ/см

Приведенные зависимости были сняты при однородном поле.

При неоднородном поле, например, в случае игольчатых электродов, ударная ионизация захватывает лишь области, расположенные около электродов; по мере удаления от острия напряженность поля убывает, поэтому процесс ионизации приостанавливается. Нередко ток сопровождается прорастанием канала на некоторую глубину диэлектрика. По данным Н.М. Торбина диаметр канала при испытаниях каменной соли составляет 0,5—2 мк, а плотность тока может достигать 10⁴ а/см². При столь высокой плотности тока температура в канале может достигать нескольких тысяч градусов, что приводит к разогреванию и плавлению диэлектрика.

В головке канала значение напряженности поля наибольшее, и там может происходить термическая ионизация; имеется вероятность образования фотонов с большой энергией, которые способны вызывать ионизацию; эти процессы способствуют дальнейшему углублению канала.

В кристаллических диэлектриках при положительном острие наблюдается большое количество разветвлений, расходящихся от основного канала.

Значение тока при сильном поле связано с толщиной диэлектрика и с ее увеличением растет (Рис. 5‑18).

Ток, протекающий в этой стадии, зависит от строения и состава диэлектрика, возрастая с увеличением его электрической прочности. Ток в стекле с увеличением толщины возрастает быстрее, чем в щелочно-галоидных кристаллах, а значения тока для NaCI больше, чем для КС1 и КВг. Эти факторы указывают на наличие ионизационных процессов, так как с увеличением плотности вещества при одной и той же толщине число ионизационных столкновений электронов увеличивается, что приводит к увеличению тока в диэлектриках с более плотной структурой.

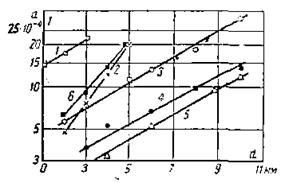Рис. 5‑18 Зависимость тока от толщины диэлектрика при неоднородном сильном поле. I — NaCI острие минус; 2 — стекло острие плюс; 3 — NaCI острие плюс; 4 — КС1 острие плюс; 5 — КВг острие плюс; 6 — стекло острие минус

При электродах игла — плоскость канал развивается у острия, а при электродах игла-игла — от обоих электродов. Когда канал достигает противоположного электрода или встречается с каналом, идущим от противоположного электрода, на осциллограмме отмечается резкое нарастание тока и снижение напряжения, характерное для пробоя.

Таким образом, процессы в твердых диэлектриках при толщинах свыше примерно 0,1 мм имеют большую аналогию с процессами, наблюдаемыми в газообразных и жидких диэлектриках при сильных электрических полях.

При сильных электрических полях также наблюдается влияние температуры на электропроводность твердых диэлектриков.

Для щелочно-галоидных кристаллов, согласно Г.А. Андрееву, электропроводность тем выше, чем меньше энергия решетки. Это справедливо не только при низких, но и при высоких температурах.

На Рис. 5‑19 приведены зависимости тока в кристаллах в сильном поле от энергии решетки при высоких температурах; из этих кривых следует, что кристаллам с меньшей энергией решетки соответствует больший ток. Зависимость тока от энергии решетки кристаллов NaCI, KCI и KBr прямолинейна. Цифры, обозначающие прямые на графиках, соответствуют шкалам тока с тем же цифровым обозначением.

Электропроводность твердого диэлектрика в сильных полях с ростом температуры возрастает по экспоненциальному закону. Согласно теории пробоя диэлектриков Фрёлиха, это рассматривается как следствие электронного процесса. Энергетическое равновесие в диэлектрике устанавливается за счет неупругих столкновений между электронами, находящимися в зоне проводимости. Взаимодействие электрона с решеткой сопровождается поглощением или выделением им энергии.

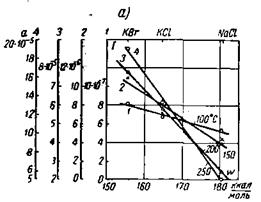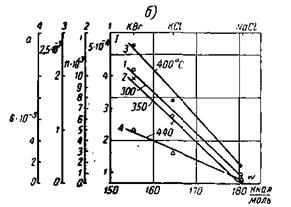Рис. 5‑19 Зависимость тока в кристаллах в сильном поле от энергии решетки для образцов толщиной 0,1мм для температур: а — от 100 до 250°С; б — от 200 до 446°С (по Г. А. Андрееву)

Передача энергии от электронов к решетке осуществляется за счет превышения температуры электронов Т_э над температурой решетки Т_р.

При достаточной величине напряженности поля Е электроны, находящиеся в зоне проводимости, накапливают энергию, необходимую для возбуждения и ионизации атомов решетки, что в конце концов приводит к пробою диэлектрика.

При температуре Т_э, выше некоторой критической Т_кр, число электронов в зоне проводимости и на локальных уровнях велико. Взаимодействие их с решеткой происходит более интенсивно. В зоне проводимости диэлектрика количество электронов N₁ возрастает с температурой Т по закону

.

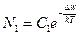При напряженности поля Е, заряде электрона q_э и его эффективной массе т* средняя скорость электрона

,

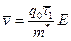где 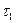— среднее время между столкновениями для электрона зоны проводимости.

Плотность тока

.

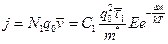Таким образом, по Фрёлиху ток в твердом диэлектрике в сильных полях обусловлен электронной проводимостью, ионной составляющей пренебрегается; проводимость с увеличением температуры возрастает по экспоненциальному закону.