Дифференцируемость функции комплексной переменной.
3.1.1. Определение производной. Аналитичность ФКП.Пусть w = f(z) определена, однозначна и принимает собственные значения в окрестности точки 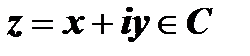 . Производной функции w = f(z) в точке z называется предел
. Производной функции w = f(z) в точке z называется предел 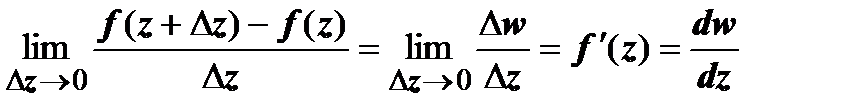 . Функция, имеющая конечную производную в точке z, называется дифференцируемой в этой точке.
. Функция, имеющая конечную производную в точке z, называется дифференцируемой в этой точке.
В этом определении важно, что стремление 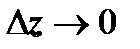 может проходить по любому пути. Как мы увидим дальше, вследствие этого обстоятельства существование производной f’(z) не сводится к существованию частных производных функций u(x, y) и v(x, y), а требует некоторых дополнительных условий. Сейчас мы дадим определение основного в теории ФКП понятия - аналитичности функциив точке и в области.
может проходить по любому пути. Как мы увидим дальше, вследствие этого обстоятельства существование производной f’(z) не сводится к существованию частных производных функций u(x, y) и v(x, y), а требует некоторых дополнительных условий. Сейчас мы дадим определение основного в теории ФКП понятия - аналитичности функциив точке и в области.
Определение. Однозначная функция называется аналитической (регулярной, голоморфной) в точке z, если она дифференцируема в некоторой окрестности этой точки.
Однозначная функция называется аналитической в области D,если она аналитична в каждой точке этой области.
Примеры.1.f(z) = z2.В этом случае 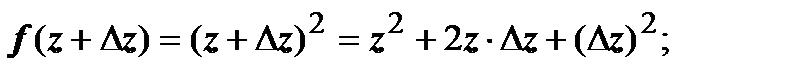
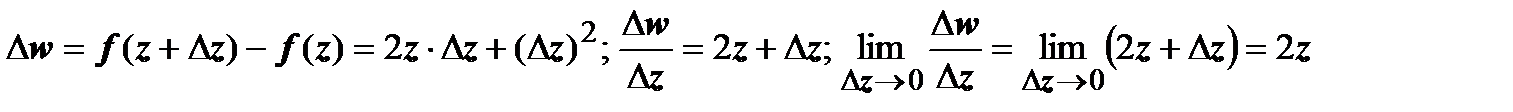 .Таким образом , эта функция дифференцируема в любой точке, и её производная равна 2z.
.Таким образом , эта функция дифференцируема в любой точке, и её производная равна 2z.
| С |
| х |
| у |
| z |
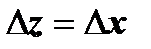
|
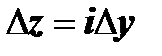
|
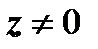 . Будем стремить
. Будем стремить 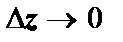 по двум путям: по прямой, параллельной действительной оси Ох (в этом случае
по двум путям: по прямой, параллельной действительной оси Ох (в этом случае 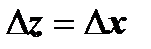 ), и по прямой, параллельной мнимой оси Оу (в этом случае
), и по прямой, параллельной мнимой оси Оу (в этом случае 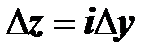 ). В первом случае
). В первом случае 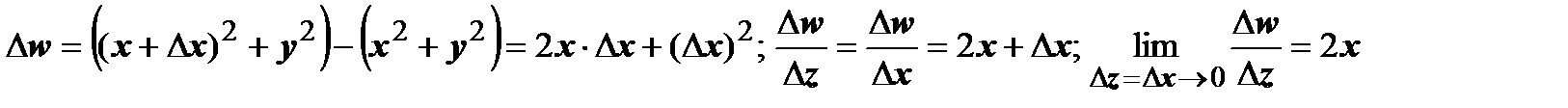 ,во втором
,во втором 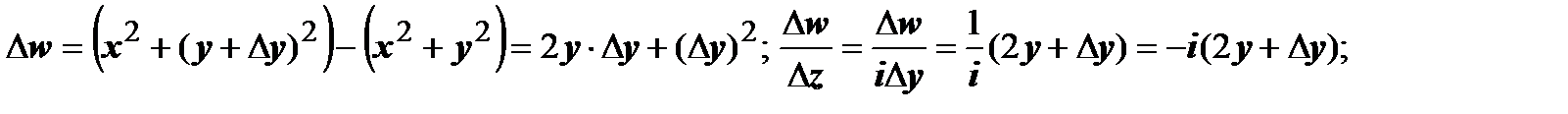
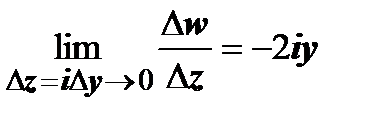 . Эти пределы равны, только если
. Эти пределы равны, только если 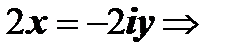
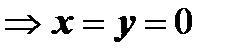 . Таким образом, функция f(z) = | z |2 = x2 + y2может быть дифференцируема в единственной точке z = 0, во всех остальных точках пределы
. Таким образом, функция f(z) = | z |2 = x2 + y2может быть дифференцируема в единственной точке z = 0, во всех остальных точках пределы 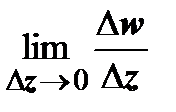 различны в зависимости от способа стремления
различны в зависимости от способа стремления 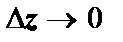 , т.е.
, т.е. 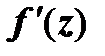 не существует.
не существует.
3.1.2. Условия Коши-Римана (Даламбера-Эйлера).Сейчас мы сформулируем и докажем важнейшую в теории ФКП теорему о необходимых и достаточных условиях дифференцируемости (а, следовательно, аналитичности) функции.
Для того, чтобы функция w = f(z) = u(x, y) + iv(x, y) была дифференцируема в точке z = x + iy, необходимо и достаточно, чтобы функции u(x, y) = Re f(z) и v(x, y) = Im f(z) были дифференцируемы в точке (х,у), и чтобы в этой точке выполнялись соотношения
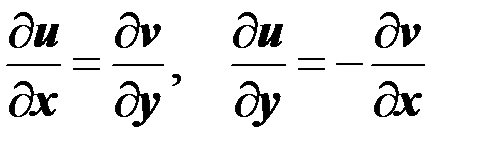 .
.
Доказательство. Необходимость. Здесь мы применим идею, которой воспользовались, когда доказывали, что функция f(z) = | z |2 = x2 + y2не имеет производных в точках 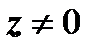 : подойдём к точке z двумя путями - по направлениям
: подойдём к точке z двумя путями - по направлениям 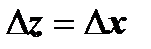 (
( 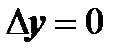 ) и
) и 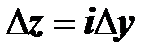 (
( 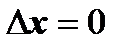 ).
).
В первом случае: 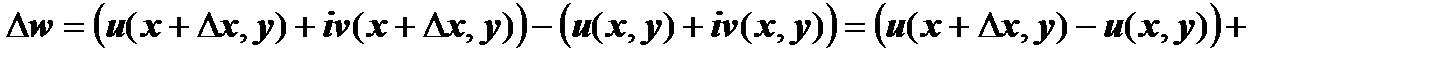
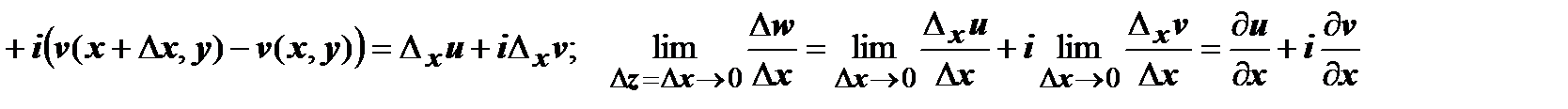 .
.
Во втором случае: (напомню, что 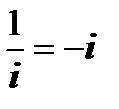 )
)
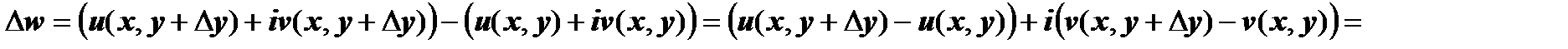
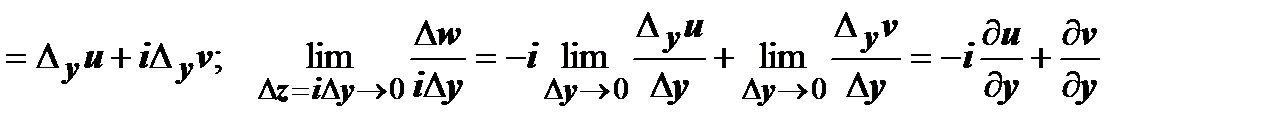 . Пределы должны быть равны, поэтому
. Пределы должны быть равны, поэтому 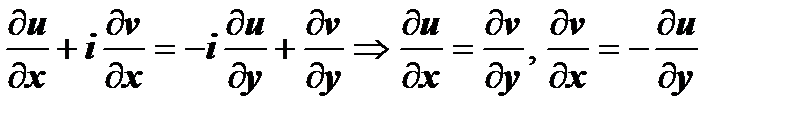 .
.
Достаточность. По предположению теоремы, функции u(x, y), v(x, y) дифференцируемы в точке (х,у), поэтому 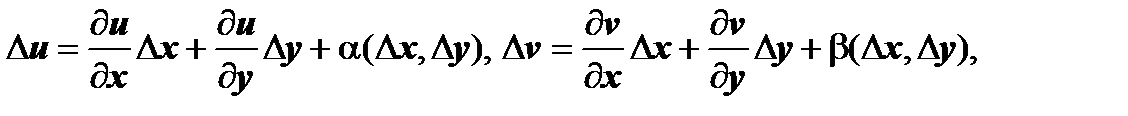 где
где 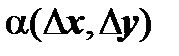 ,
,
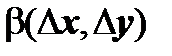 - бесконечно малые более высокого порядка по сравнению с
- бесконечно малые более высокого порядка по сравнению с 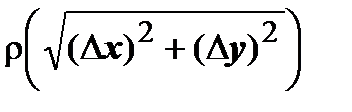 , т.е.
, т.е. 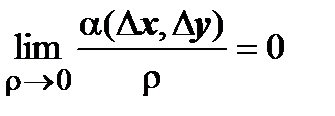 ,
, 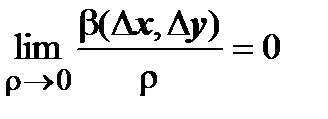 . Найдём
. Найдём 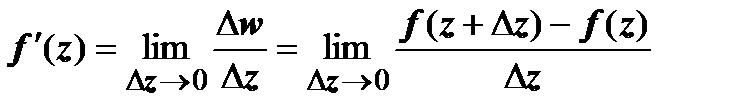 .
. 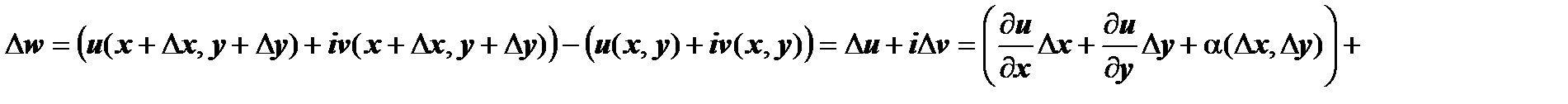
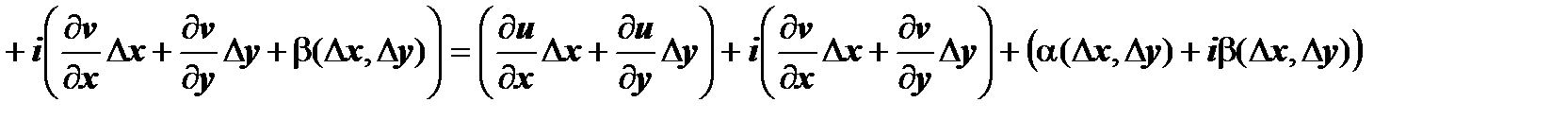 .
.
Последнее слагаемое - бесконечно малая высшего порядка по сравнению с 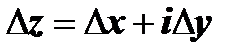 :
: 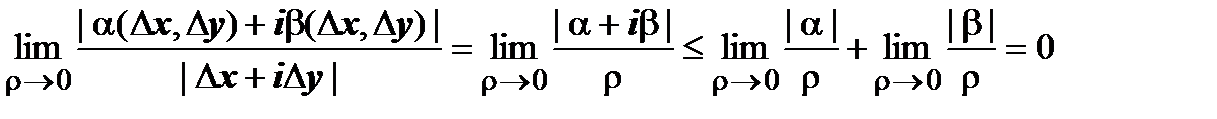 ; далее, в предыдущих слагаемых, пользуясь формулами Коши-Римана, оставим только частные производные по х, т.е. заменим
; далее, в предыдущих слагаемых, пользуясь формулами Коши-Римана, оставим только частные производные по х, т.е. заменим 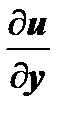 на
на 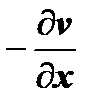 ,
, 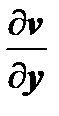 на
на 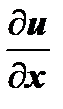 ; тогда
; тогда 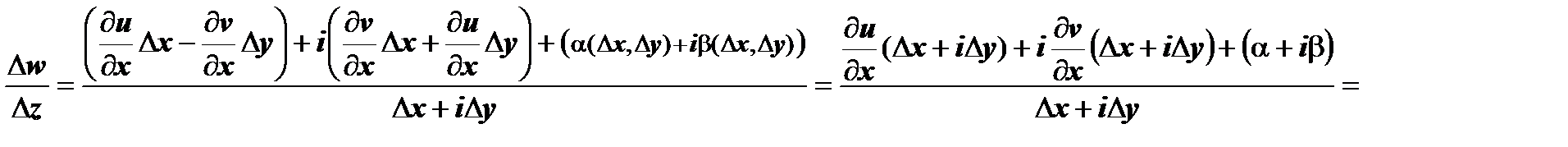
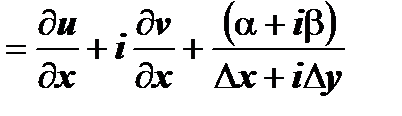 . Отсюда следует, что существует
. Отсюда следует, что существует 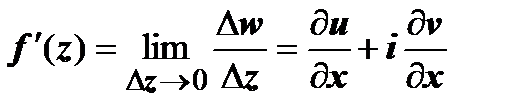 , т.е. функция дифференцируема в точке (х,у).
, т.е. функция дифференцируема в точке (х,у).
Производная дифференцируемой функции может находиться по любой из формул 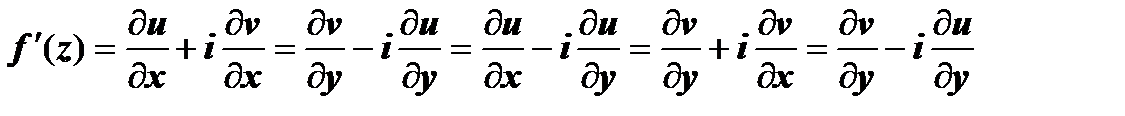 , эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа:
, эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа:  (в точках, где
(в точках, где 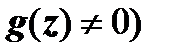 .
.
Дата добавления: 2019-12-09; просмотров: 588;











