Схема независимых испытаний Бернулли. Полиноминальное распределение
Предположим, что производятся независимо друг от друга nиспытаний, в каждом из которых возможны только 2 исхода: успех и неудача («У»,»Н»). Причём вероятность успеха Р(У)=p, Р(Н)=q , p+q=1.
Определение 10.1. Последовательность 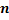 испытаний называется испытаниями Бернулли, если эти испытания независимы, в каждом из них возможны 2 исхода, причём вероятности этих исходов не меняются от испытания к испытанию.
испытаний называется испытаниями Бернулли, если эти испытания независимы, в каждом из них возможны 2 исхода, причём вероятности этих исходов не меняются от испытания к испытанию.
В nиспытаниях Бернулли элементарным исходом является:
(ω1, ω2,…, ωn), где ωi 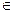 {У,Н}, i
{У,Н}, i 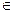 {1,…,n}.
{1,…,n}.
Всего таких исходов 2n. Поскольку испытания независимы, то:
Р(ω1, ω2,…, ωn)= Р(ω1)P(ω2)…P(ωn).
Обозначим через Pn(k) вероятность того, что в n испытаниях Бернулли произошло ровно k успехов. Тогда
Pn(k)=Р{(У,…,У,Н,…,Н),(У,…,У,Н,У,Н,…,Н),…,(Н,…,Н,У,…У)}=
= pkqn-k + pkqn-k + …+ pkqn-k = 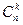 pkqn-k.
pkqn-k.
Таким образом получим
Pn(k)= 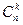 pkqn-k, k
pkqn-k, k 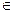 {0,…,n} , p+q=1 – формула Бернулли.
{0,…,n} , p+q=1 – формула Бернулли.
Пример 10.2. Двое равных по силам шахматистов играют в шахматы. Что вероятнее: выиграть одну партию из двух или две из четырёх? Ничьи во внимание не принимаются.
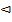 p=q=
p=q= 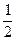 , P2(1)=
, P2(1)= 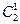 ∙
∙ 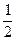 ∙
∙ 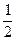 =
= 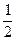 =
= 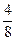 ;
;
P4(2)= 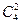 ∙(
∙( 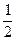 )2∙(
)2∙( 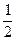 )2=6∙
)2=6∙ 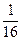 =
= 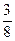 ;
;
Таким образом P2(1)> P4(2). 
Полиноминальное распределение
Предположим, что производится независимо друг от друга n испытаний, в каждом из которых возможны k исходов E1, E2,…, Ek. Вероятность этих исходов обозначим P(Ei)=pi, i 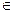 {1,…,k}. Причём
{1,…,k}. Причём 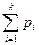 =1, k>2.Вероятность того, что в n испытаниях исход E1 появится r1 раз, E2
=1, k>2.Вероятность того, что в n испытаниях исход E1 появится r1 раз, E2 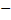 r2 раз, …, E1 – rk раз, где
r2 раз, …, E1 – rk раз, где 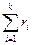 =n, находится по формуле:
=n, находится по формуле:
P(r1, r2,…, rk)= 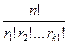
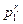
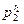 …
… 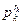 ,
, 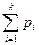 =1,
=1, 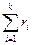 =n – формула полиноминального распределения.
=n – формула полиноминального распределения.
Замечание 10.3. Формула полиноминального распределения обобщает формулу Бернулли на случай более 2 исходов в каждом испытании.
Пример 10.4.В урне 3 шара: белый, красный, синий. Из урны 5 раз наудачу извлекаются шары с возвращением. Найти вероятность того, что белый шар извлечён 3 раза, а красный и синий –по одному разу.
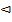 Поскольку p1= p2= p3=
Поскольку p1= p2= p3= 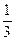 ; r1 =3, r2=1, r3 =1.
; r1 =3, r2=1, r3 =1.
Тогда P5(3,1,1)= 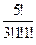 ∙(
∙( 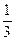 )3∙
)3∙ 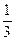 ∙
∙ 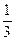 = 20∙
= 20∙ 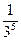 =
= 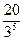 =
= 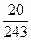 .
. 
Дата добавления: 2016-06-15; просмотров: 2028;











