УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА Вывод уравнения колебания струны
Рассмотрим натянутую струну, закрепленную на концах. Если струну вывести из положения равновесия (например, оттянуть ее или ударить по ней), то струна начнет колебаться.
Будем рассматривать только поперечные колебания, т.е. такие, когда движение всех точек струны происходит в одной плоскости и в направлении, перпендикулярном положению равновесия. Если положение равновесия принять за ось 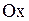 , то процесс будет характеризоваться одной скалярной величиной
, то процесс будет характеризоваться одной скалярной величиной 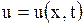 - отклонением от положения равновесия точки струны
- отклонением от положения равновесия точки струны 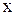 в момент времени
в момент времени 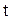 . Поэтому, чтобы знать положение любой точки
. Поэтому, чтобы знать положение любой точки 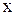 струны в произвольный момент времени
струны в произвольный момент времени 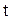 , нужно найти зависимость
, нужно найти зависимость 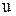 от
от 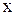 и
и 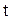 , т.е. найти функцию
, т.е. найти функцию 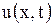 .
.
 При каждом фиксированном значении
При каждом фиксированном значении 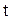 график функции
график функции 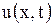 представляет форму струны в этот момент времени. Частная производная
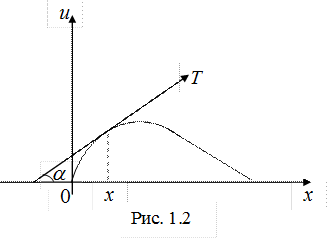
представляет форму струны в этот момент времени. Частная производная 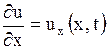 дает при этом угловой коэффициент касательной в точке с абсциссой
дает при этом угловой коэффициент касательной в точке с абсциссой 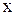 (рис. 1.2). При постоянном значении
(рис. 1.2). При постоянном значении 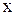 функция
функция 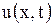 дает закон движения точки с абсциссой
дает закон движения точки с абсциссой 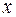 вдоль прямой, параллельной оси
вдоль прямой, параллельной оси 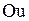 , производная
, производная 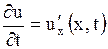 - скорость этого движения, а вторая производная
- скорость этого движения, а вторая производная 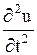 - ускорение. Задача состоит в том, чтобы составить уравнение, которому должна удовлетворять функция
- ускорение. Задача состоит в том, чтобы составить уравнение, которому должна удовлетворять функция 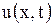 .
.
Для решения данной задачи сделаем несколько предположений.
А. Будем считать струну абсолютно гибкой, т.е. не сопротивляющейся изгибу; это означает, что если удалить часть струны, лежащую по одну сторону от какой-либо ее точки, то сила натяжения 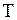 , заменяющая действие удаленной части, всегда будет направлена по касательной к струне (рис. 1.2).
, заменяющая действие удаленной части, всегда будет направлена по касательной к струне (рис. 1.2).
Б. Струна упругая, вследствие чего возникают лишь силы натяжения, которые подчинены закону Гука: натяжение струны пропорционально ее удлинению.
В. Пренебрегаем толщиной струны, т.е. считаем ее нитью.
Г. На струну в плоскости колебания действуют силы, параллельные оси 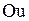 , которые могут меняться вдоль струны со временем. Будем считать, что эти силы непрерывно распределены вдоль струны. Величину силы, направленной вверх, условимся считать положительной, а вниз – отрицательной. Плотность распределения этих сил обозначим через
, которые могут меняться вдоль струны со временем. Будем считать, что эти силы непрерывно распределены вдоль струны. Величину силы, направленной вверх, условимся считать положительной, а вниз – отрицательной. Плотность распределения этих сил обозначим через 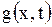 . Если единственной внешней силой является вес струны, то
. Если единственной внешней силой является вес струны, то 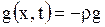 , где
, где 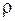 - плотность струны, а
- плотность струны, а 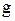 - ускорение силы тяжести. Силами сопротивления среды, в которой колеблется струна, пренебрегаем.
- ускорение силы тяжести. Силами сопротивления среды, в которой колеблется струна, пренебрегаем.
Д. Будем рассматривать только малые колебания струны. Математически это означает, что отклонения 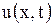 малы и, следовательно, угловой коэффициент струны
малы и, следовательно, угловой коэффициент струны 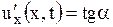 (угол
(угол 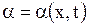 ) в любой момент времени
) в любой момент времени 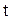 столь мал, что квадратом углового коэффициента
столь мал, что квадратом углового коэффициента 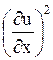 можно пренебречь в сравнении с единицей).
можно пренебречь в сравнении с единицей).
Е. Величину силы натяжения 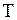 можно считать постоянной, не зависящей ни от точки
можно считать постоянной, не зависящей ни от точки 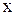 ее приложения, ни от времени
ее приложения, ни от времени 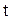 .
.
Дадим обоснование этому допущению. Выделим произвольный участок 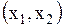 струны, который при колебании струны деформируется в участок
струны, который при колебании струны деформируется в участок 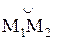 (рис. 1.3). Длина
(рис. 1.3). Длина 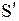 дуги
дуги 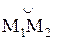 в момент времени
в момент времени 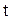 равна:
равна:
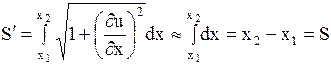 .
.
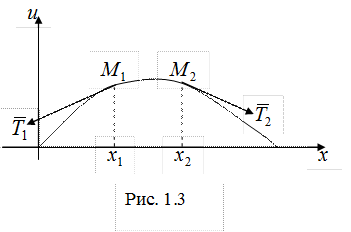 Следовательно, при предположении п. Д в процессе колебания удлинения участков струны не происходит. Отсюда, в силу закона Гука, следует, что величина натяжения
Следовательно, при предположении п. Д в процессе колебания удлинения участков струны не происходит. Отсюда, в силу закона Гука, следует, что величина натяжения 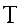 в каждой точке остается неизменной во времени. Покажем также, что натяжение не зависит и от
в каждой точке остается неизменной во времени. Покажем также, что натяжение не зависит и от 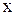 , т.е.
, т.е. 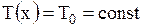 . Действительно, на участок струны
. Действительно, на участок струны 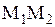 действуют силы натяжения
действуют силы натяжения 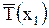 и
и 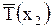 , направленные по касательным к струне в точках
, направленные по касательным к струне в точках 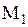 и
и 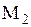 , внешние силы и силы инерции. Воспользуемся принципом кинетостатики, на основании которого все силы должны уравновешиваться (принцип Даламбера). Согласно принципу Даламбера сумма проекций на ось
, внешние силы и силы инерции. Воспользуемся принципом кинетостатики, на основании которого все силы должны уравновешиваться (принцип Даламбера). Согласно принципу Даламбера сумма проекций на ось 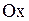 всех сил равна нулю. Так как рассматриваются только поперечные колебания, то внешние силы и силы инерции направлены по оси
всех сил равна нулю. Так как рассматриваются только поперечные колебания, то внешние силы и силы инерции направлены по оси 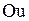 и потому сумма проекций сил запишется так:
и потому сумма проекций сил запишется так:
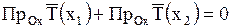 .
.
Но 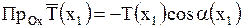 ,
, 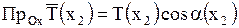 , где
, где 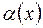 - угол между касательной в точке с абсциссой
- угол между касательной в точке с абсциссой 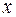 к струне в момент
к струне в момент 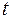 с положительным направлением оси
с положительным направлением оси 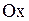 . Итак, имеем
. Итак, имеем
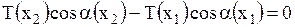 .
.
Учитывая малость колебаний, 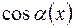 можно заменить:
можно заменить:
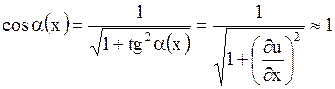 .
.
Тогда получим, что 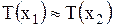 . Отсюда, ввиду произвольности
. Отсюда, ввиду произвольности 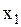 и
и 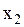 , следует, что величина натяжения не зависит от
, следует, что величина натяжения не зависит от 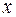 . Таким образом, можно считать, что
. Таким образом, можно считать, что 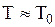 при всех значениях
при всех значениях 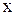 и
и 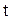 .
.
Перейдем теперь к выводу уравнения колебания струны при сделанных допущениях (см. пп. А – Е).
Составим сумму проекций всех сил на ось 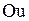 : сил натяжения, внешних сил и сил инерции.
: сил натяжения, внешних сил и сил инерции.
Сумма проекций на ось 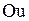 сил натяжения, действующих в точках
сил натяжения, действующих в точках 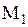 и
и 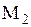 , запишется в виде
, запишется в виде
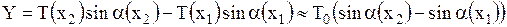 .
.
Вследствие предположения п. Д
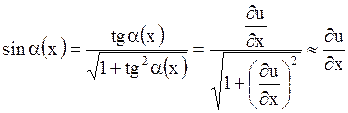 .
.
Следовательно, 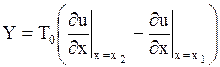 .
.
Замечая, что 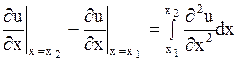 ,
,
окончательно получаем
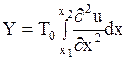 . .
| (1.112) |
Обозначим через 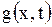 внешнюю силу, действующую на струну параллельно оси
внешнюю силу, действующую на струну параллельно оси 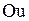 и рассчитанную на единицу длины. Тогда проекция на ось
и рассчитанную на единицу длины. Тогда проекция на ось 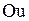 внешней силы, действующей на участок
внешней силы, действующей на участок 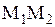 , будет равна
, будет равна
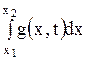 . .
| (1.113) |
Обозначим через 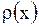 линейную плотность струны; тогда на участок
линейную плотность струны; тогда на участок 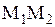 будет действовать сила инерции, равная
будет действовать сила инерции, равная
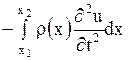 . .
| (1.114) |
Приравнивая к нулю сумму проекций всех сил (1.112), (1.113), (.114), получим
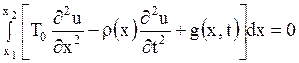 . .
| (1.115) |
Если подынтегральная функция непрерывна, то из равенства нулю интеграла следует, что функция тождественно равна нулю в этой области. Предполагая существование и непрерывность вторых производных функции 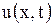 , а также непрерывность функций
, а также непрерывность функций 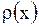 и
и 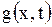 , заключаем, что в силу произвольности
, заключаем, что в силу произвольности 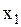 и
и 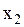 , подынтегральная функция должна равняться нулю для всех
, подынтегральная функция должна равняться нулю для всех 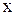 и
и 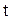 :
:
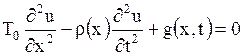
или
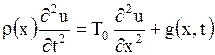 . .
| (1.116) |
Это и есть искомое уравнение колебаний струны.
Если струна однородная, т.е. 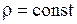 , то уравнение (1.116) обычно записывается в виде
, то уравнение (1.116) обычно записывается в виде
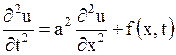 , ,
| (1.117) |
где 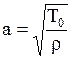 ,
, 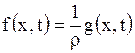 .
.
Неоднородное уравнение (1.117) называется уравнением вынужденных колебаний струны; если 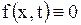 , т.е. внешняя сила отсутствует, то уравнение (1.117) становится однородным:
, т.е. внешняя сила отсутствует, то уравнение (1.117) становится однородным:
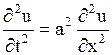 . .
| (1.118) |
Уравнение (1.118) описывает свободные колебания струны без воздействия внешних усилий.
Уравнение (1.117) – одно из простейших уравнений гиперболического типа и в то же время одно из важнейших дифференциальных уравнений математической физики. К нему сводится не только рассмотренная задача, но и многие другие.
Дата добавления: 2018-11-26; просмотров: 752;










