Матричные методы умножения.
Кроме рассмотренных методов ускоренного умножения существуют методы умножения, основанные на использовании матриц промежуточных результатов.
Пусть имеем сомножители: Мн = А = аn ... a2 a1
Мт = B = bn ... b2 b1
Рассмотрим схему традиционного (“школьного”) алгоритма умножения (Б).
А = аn ... a2 a1
* B = bn ... b2 b1
 anb1 ... a3b, a2b1, a1b1
anb1 ... a3b, a2b1, a1b1
+anb2 . . .a2b2, a1b2
+ . . .
anbn ... a2bn, a1bn
 C = C2n . . . . C2 C1
C = C2n . . . . C2 C1
Рассмотренная схема умножения может быть представлена в виде матрицы.
Таблица 3
| an | . . . | a2 | a1 | |
| b1 | an b1 | . . . | a2 b1 | a1 b1 |
| b2 | an b2 | . . . | a2 b2 | a1 b2 |
| . . . | . . . | |||
| bn | an bn | . . . | a2 bn | a1 bn |

Каждый элемент ai bj ( i, j = 1, n) принимает значение 0 или 1. Произведение A∙B может быть получено, если суммировать элементы матрицы (по диагонали).


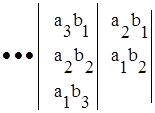
Для суммирования по столбцам могут быть использованы счетчики. Однако при достаточно большом значении величины n потребуются счетчики с большим числом входов, что существенно увеличит время сложения. Но этот принцип умножения может быть реализован на устройствах имеющих не более трех входов. В качестве их могут быть использованы одноразрядные двоичные сумматоры и полусумматоры.
На рис. 10 приведена структурная схема устройства умножения для реализации матричного алгоритма.
Реализация методов матричного умножения требует большего количества оборудования, чем метод последовательного умножения и дает больший выигрыш во времени. В связи с увеличением степени интеграции элементной базы ограничения по качеству оборудования становятся не столь строгими.
Дата добавления: 2022-02-05; просмотров: 392;











