Умножение в дополнительных кодах.

Умножение чисел в дополнительных кодах может выполняться по любому из рассмотренных выше четырех алгоритмов, но отличается тем, что для получения верного результата необходимо вводить поправки. Умножение правильных дробей и целых чисел имеет некоторые различия.

Рассмотрим вначале умножение дробных чисел. Возможны четыре случая знакосочетания сомножителей.

1) Мн>0,

Мт>0,

в этом случае дополнительный код сомножителей совпадает с прямым кодом и умножение выполняется по правилам умножения в прямых кодах, в результате чего получается верный результат.

2) Мн>0,

Мт<0,

так как Мн и Мт имеют разные знаки, то результат будет иметь отрицательный знак. Следовательно, результат должен быть представлен в дополнительном коде [Мн∙Мт]_доп=2-Мн∙Мт. Для формирования произведения выполним умножение Мн на Мт’ (дополнение)

Мн∙Мт’= Мн ∙(1 - Мт)= Мн - Мн∙Мт.

Таким образом, погрешность Δ умножения равна разности [Мн∙Мт]_доп- и Мт∙Мн’

Δ=2-Мн∙Мт- Мн - Мн∙Мт=2-Мн=[-Мн]_доп=[ [Мн]_доп]_доп

и должна быть внесена в полученный результат в качестве поправки.

Пример: Мн = 0,1011 (алгоритм умножения А)

Мт = - 0,1101

Δ= [- М_H]_доп = 1.0101

[- М_T]_доп = 1.0011

0.0000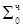

0.1011 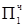= Мн b₄

0.1011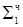

0.0101 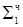1 ∙ 2^-1

0.1011 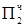= Мн b₃

1.0000 1 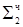(произошло переполнение)

0.1000 01 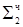∙ 2^-1 (коррекция)

0.010 0001 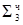∙ 2^-1 ( 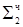∙ 2^-1) ∙ 2^-1

0.0010 0001 ∙ 2^-1 (( 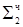∙ 2^-1 )∙ 2^-1)∙ 2^-1

1.0101 Δ = [- М_H]_доп (поправка)

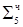1.0111 0001 =[M_H ∙ M_T]_доп

- 1000 1111 M_H ∙ M_T

В этом примере, а также в некоторых примерах следующих ниже происходит переполнение разрядной сетки, в результате которого искажаются и знаковая и значащая часть числа. Для коррекции (восстановления верного значения) производится не модифицированный сдвиг. В результате этого знаковый разряд сдвигается в значащую часть, а знаковый разряд меняет свое значение на противоположное.

3) Mн<0,

Mт>0,

аналогично предыдущему случаю

[Мн∙Мт]_доп=2-Мн∙Мт

Мн’∙Мт= (1 - Мн)∙Мт= Мт - Мн∙Мт

Таким образом, погрешность умножения равна разности [Мн Мт]_доп и Мт∙Мн’.

Δ=2-Мн∙Мт- Мт - Мн∙Мт=2-Мт=[-Мт]_доп=[ [Мт]_доп]_доп

Использовать этот вариант неудобно, так как нужно вводить поправку [-Mт]_доп в конце умножения, а в результате сдвигов М_T постепенно исчезает на регистре множителя и для поправки нужно либо вводить дополнительный регистр, либо вносить поправку в сумматор на первом такте умножения.

При этом знакосочетании возможно умножение без ввода поправки. Рассмотрим на примере умножения по алгоритму Г (это справедливо и для других алгоритмов).

Мн∙Мт = А ∙ В = [ A ∙ b₁∙ 2^-1 ]_доп + [ A ∙ b₂∙ 2^-2 ]_доп+ ... + [A∙ b_n∙ 2^-n ]_доп

На основании теоремы, что сумма дополнительных кодов есть дополнительный код, получаем [ A ∙ b₁∙ 2^-1 + A ∙ b₂∙ 2^-2 + ... + A∙ b_n∙ 2^-n ]_доп = [Мн ∙Мт]_доп.

В этом случае поправка вводится автоматически на каждом этапе умножения.

Пример: Mн = -0,1011

Mт = 0,1101

b1…b4 4

[Mн]_доп= 1.0101

0.00000000

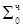
1.10101000 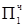= [M_H ∙ b₁ ∙ 2^-1]_доп

1.10101000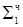

1.11010100 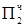= [M_H ∙ b₂ ∙ 2^-2]_доп

1.01111100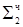

1.11110101 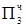= [M_H ∙ b₄ ∙ 2^-4]_доп

1.01110001 [M_H ∙ M_T]_доп

- 10001111 M_H ∙ M_T

4) M_H<0,

M_T<0,

Mн ∙ Mт = 2 - [Mн ∙ Mт]_доп

[Mн]_доп ∙ (1 - Mт) = [Mн]_доп - [M_H]_доп ∙ M_T = [Mн]_доп - [Mн ∙ Mт]_доп

Δ=2 - [Mн ∙ Mт]_gдоп - [Mн]_доп + [Mн ∙ Mт]_доп = 2 - [Mн]_доп = [[Mн]_доп]_доп

Пример: Mн = - 0,1011 умножение будем выполнять

Mт = - 0,1101 по алгоритму умножения Г.

[Mн]_доп = 1.0101

[Mт]_доп = 1.0011

Δ =[-Mн]_доп = 0.1011

0.00000000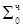

1.11101010 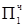= [Mн ∙ b₃ ∙ 2^-3]_доп

1.11101010

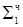
1.11110101 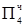= [Mн ∙ b₄ ∙ 2^-4]_доп

1.11011111

0.10110000 Δ (поправка)

0.10001111 [Mн∙ Mт]_доп

Далее коротко остановимся на умножении целых чисел. При представлении целых чисел в дополнительном коде знаковый разряд входит в число n разрядов. Следовательно, при умножении целых чисел (в отличие от дробных) в дополнительных кодах знаковый разряд участвует в умножении наряду со значащими. То есть умножение ведется на [Mт]_доп , а не на Мт’.

1) M_H > 0,

M_T > 0.

Как отмечалось выше, в этом случае умножение выполняется по правилам умножения чисел в прямых кодах.

2) М_H>0,

M_T<0,

[Мт]_доп = 2ⁿ – Мт.

Так как сомножители имеют разные знаки, то произведение Мн∙Мт<0, сле­довательно [Mн∙Мт]_доп=2²ⁿ - Mн∙Мт. Однако при умножении Мн∙[Мт]_доп получается Mн ∙(2ⁿ-Mт) =2ⁿ Mн - Mн∙Мт. Следовательно, погрешность в этом случае равна Δ=2²ⁿ–Mн∙Мт–2ⁿ Mн+Mн∙Мт =2²ⁿ–2ⁿ Mн =2²ⁿ [–Мт]_доп=2²ⁿ[ [Мт]_доп]_доп.

Пример: Mн = +110

Mт = -101

[Mн]_доп = 0.110

[Mт]_доп = 1.011

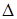= [- Mн]_доп = 1.010

0.000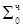

0.110 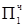= M_H∙b₄

0.110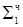

0.011 0 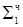∙2^-1

0.110 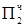= M_H∙b₃

1.001 0 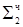(возникло переполнение)

0.100 10 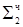∙2^-1 (коррекция)

0.010 010 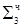∙2^-1

0.110 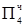= M_H∙b₁

1.000 010 (возникло переполнение)

0.100 0010 ∙2^-1 (коррекция)

1.010 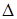(поправка)

1.110 0010 [M_H M_T]_доп

- 001 1110 M_H M_T

3) М_H<0

М_T>0

Здесь, как и при умножении дробных чисел возможны два случая:

a) с вводом поправки в получаемое произведение

[М_H]_доп = 2ⁿ - M_H

Как и ранее, требуется получить [Мн∙Мт]_доп= 2²ⁿ - Мн∙Мт. Получаем

(2ⁿ - Мн) ∙ Мт = 2ⁿ ∙ Мт - Мн∙Мт.

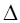= 2²ⁿ - Мн∙Мт - 2ⁿ ∙ Мт + Мн∙Мт = 2ⁿ(2ⁿ - Мт) = [Мт]_доп ∙ 2ⁿ

б) вариант без ввода поправки рассмотрим применительно к алгоритму умножения Г (как и ранее это справедливо и для других алгоритмов):

M_H∙M_T = A∙B = [A ∙ b₁ ∙ 2^-1 ]_доп + [A ∙ b₂ ∙ 2 ^-2]_доп+^- ... + [A ∙ b_n ∙ 2^-n]_доп=

=[A ∙ b₁ ∙ 2^-1 + A ∙ b₂ ∙ 2 ^–2 +^- ... + A ∙ b_n ∙ 2^-n]_доп=[Мн∙Мт]_доп.

Пример: Мн = -110 Мт = 101 [Мн]_доп = 1.010

[Мт]_доп = 0.101

b₁ ... b₄

0.0000000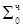

0.0000000 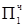= [M_H ∙ b₁]_доп ∙ 2^-1

0.0000000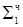

1.1101000 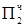= [M_H ∙ b₂]_доп ∙ 2^-2

1.1101000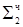

1.1111010 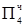= [M_H ∙ b₄]_доп ∙ 2^-4

1.1100010

4) M_H < 0

M_T < 0

При этом знакосочетании сомножителей в результате должно быть получено:

[Mн]_доп = 2ⁿ – Mн,

[Mт]_доп = 2ⁿ – Mт,

Mн ∙Mт = 2²ⁿ - [Mн Mт]_доп.

При умножении [Mн]_доп∙[Mн]_доп получается:

[Mн]_доп∙[Mн]_д =[Mн]_доп ( 2ⁿ - Mт ) = 2ⁿ [Mн]_доп -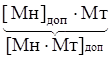

Пример: Мн = -110

Mт = -101

[Mн]_доп = 1.010

[Mт]_доп = 1.011

b₁ ... b₄

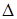= [[Mн]_доп]_доп= 0.110

При умножении используем алгоритм Г.

0.0000000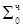

1.1010000 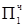= [M_H∙b₁]_доп∙2^-1

1.1010000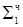

1.1110100 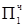= [M_H∙b₃] _доп∙2^-3

1.1000100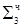

1.1111010 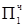= [M_H∙b₄] _доп∙2^-4

1.0111110

0.110 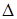(поправка)

0.0011110 M_H M_T