Основные сведения о кристаллографии
В результате различных физико-химических процессов, протекающих в недрах Земли и на ее поверхности, образуются природные химические соединения — минералы. Они встречаются в природе в двух состояниях: кристаллическом и аморфном.
В аморфных веществах отсутствует строгая закономерность в расположении молекул, атомов и ионов. В связи с этим они изотропны, не могут самоограняться и не обладают симметрией (например, стекло, пластмасса, клей, смола идругие вещества). Аморфные вещества не устойчивы и со временем кристаллизуются.
Кристалл — это природное тело, естественная многогранная форма которого обусловлена особенностями внутреннего строения. Наука, изучающая условия образования, особенности строения и состава, свойства кристаллов и кристаллических веществ, называется кристаллографией.
Кристаллы широко распространены в природе. Они слагают разнообразные горные породы. Многие вещества, окружающие нас (поваренная соль, сахар, различные химикалии, металлы идр.), также имеют кристаллическое строение.
Молекулы (атомы, ионы) в кристаллах размещаются не хаотично, а в определенном строгом порядке — параллельными рядами, причем расстояния между ними в рядах одинаковы. Эта закономерность в строении кристаллов выражается геометрически в виде пространственной решетки, которая является как бы скелетом вещества (рис. 16).
Пространственную решетку можно представить в виде бесконечно большого количества одинаковых по форме и размеру параллелепипедов, передвинутых один относительно другого и сложенных так, что они выполняют пространство без промежутков. Вершины параллелепипедов, в которых находятся атомы, ионы или молекулы, называются узлами пространственной решетки, а прямые линии, проведенные через них,— рядами решетки.
Упорядоченное внутреннее строение кристаллических веществ обусловливает их основные свойства: анизотропность, способность самоограняться и тип симметрии.
Анизотропность (т.е. неравносвойственность) обусловлена одинаковыми расстояниями между атомами, ионами,илимолекулами в параллельных направлениях и неодинаковыми—в непараллельных. В результате одно и то же физическое свойство кристаллического вещества изменяется по значению показателей в разных направлениях. Характерным примером являются слюды: мусковит и биотит. Кристаллические пластинки этих минералов легко расщепляются по плоскостям, параллельным пластинчатости. В поперечных направлениях расщепить пластинку слюды значительно труднее.
Изотропные тела обладают одинаковыми свойствами во всех направлениях.
Способность самоограняться. Поверхности кристаллов ограничиваются плоскостями, которые называются гранями. Места соединения граней называются ребрами, точки пересечения которых называются вершинами.

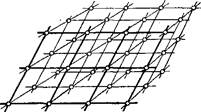
Рис 15. Пространственнаярешетка Рис 16 . Кристаллы поваренной соли
(I) и магнетита (2).
а — грани; б — ребра; в —вершина
Во многих случаях кристаллы веществ не имеют ясно выраженной формы, но при свободном росте они принимают вид правильных многогранников.
Симметрия - закономерная повторяемость в пространстве одинаковых частей тела или фигуры (углов, граней, ребер), а также зеркальное равенство их частей (одни части кристалла как бы являются зеркальным отражением других). Это свойство обусловлено закономерностью внутреннего строения кристаллов. Симметрия кристаллов выявляется при помощи воображаемых образов, называемых элементами симметрии: плоскостей, прямых линий, точек. Все кристаллы являются телами симметричными.
Закон постоянства углов. В любом кристаллическом многограннике угол между двумя пересекающимися гранями называется гранным углом. В зависимости от поступления питающего раствора размер, величина, число и форма граней в кристалле одного и того же вещества могут меняться за счет неодинаковой скорости роста разных граней. Так, в процессе роста одни грани получают преимущественное развитие, а другие могут совсем исчезнуть. Исчезают грани, обладающие большей скоростью роста. Таким образом облик растущего кристалла может совершенно измениться, но гранные углы остаются неизменными. В этом заключается один из основных законов кристаллообразования — закон постоянства гранных углов, который формулируется следующим образом: углы между соответственными гранями во всех кристаллах одного и того же вещества при одинаковых условиях давления и температуры постоянны.
 Измерение гранных углов кристаллов различных минералов имеет большое значение при их диагностике. Приборы, с помощью которых устанавливается величина гранных углов, называются гониометрами. Самый простой гониометр, употребляемый для приблизительных измерений гранных углов, называется прикладным гониометром (рис. 17). Для точных измерений углов и для мелких кристаллов применяют отражательные гониометры.
Измерение гранных углов кристаллов различных минералов имеет большое значение при их диагностике. Приборы, с помощью которых устанавливается величина гранных углов, называются гониометрами. Самый простой гониометр, употребляемый для приблизительных измерений гранных углов, называется прикладным гониометром (рис. 17). Для точных измерений углов и для мелких кристаллов применяют отражательные гониометры.
Симметрия кристаллов. При вращении большинства кристаллов вокруг какой-либо оси наблюдается закономерная повторяемость одинаковых углов, граней, ребер, а также зеркальное равенство частей фигуры (одни части кристаллов как бы зеркально отражают другие). Это свойство обусловлено закономерностью внутреннего строения кристаллов.
Рис 17
Принято различать следующие элементы симметрии: плоскости (Р), оси (L), центр симметрии (С).
Плоскость симметрии (Р) — мысленно проведенная плоскость, которая делит кристалл на две равные части, причем одна из них как бы зеркально отражает другую.
.Цифра перед буквой «Р» показывает число плоскостей симметрии кристаллического многогранника. В кристалле может быть от одной до девяти плоскостей симметрии, но многие кристаллы вообще не имеют ни одной плоскости симметрии.
Ось симметрии (X) — прямая линия, при вращении вокруг которой на 360° кристалл несколько раз повторяет свое начальное положение в пространстве. Число повторений начального положения кристалла при вращении вокруг оси симметрии называется ее порядком. Порядок оси можно узнать, разделив 360° на величину угла, на который надо повернуть фигуру, чтобы повторилось ее начальное положение в пространстве. Например, углы поворота фигуры: 180, 120, 90, 60°. Этим углам соответствуют оси симметрии:
360 / 180 = 2 – ось второго порядка (L2);
360 / 120 = 3 – ось третьего порядка (L3);
360 / 90 = 4 – ось четвертого порядка (L4);
360 / 60 = 6 – ось шестого порядка (L6).
В одном и том же кристалле может быть несколько осей симметрии одного порядка или разных порядков.
Центр симметрии (С)— это точка внутри кристалла, от которой на одинаковых расстояниях в диаметрально-противоположных направлениях располагаются одинаковые части фигуры. Внешним выражением наличия центра симметрии в кристалле является присутствие параллельных граней и ребер. Некоторые кристаллы не имеют центра симметрии.
Плоскость, ось и центр симметрии находятся в кристаллах во взаимной связи и сочетания их весьма ограничены. Возможны только 32 комбинации элементов симметрии. Каждая комбинация соответствует определенным кристаллографическим классам или видам симметрии. Кристаллографические классы (виды симметрии) объединяются в семь групп — сингоний («сингония» по гречески — сходноугольность): триклинная, моноклинная,ромбическая, тригональная, гексональная, тетрагональная (квадратная), кубическая.
Триклинная, моноклинная и ромбическая сингонии называются низшими, так как они не имеют осей симметрии выше второго порядка (L2)Тригональная, гексагональная и тетрагональная сингонии называются средними; наряду с осями симметрии второго порядка они имеют одну ось симметрии высшего порядка, соответственно L3, L6, L4. Кубическая сингония характеризуется несколькими осями симметрии высшего порядка (Х3, Li) и является высшей сингонией.
Соотношение элементов симметрии, характеризующих кристаллы определенной сингонии, выражается формулой. Формулы, отражающие наиболее полное развитие элементов симметриив кристаллах каждой сингонии, приведены в табл. 3.
Таблица 3
Характеристика кристаллографических сингоний
| Категория сингонии | Сингония | Характерные элементы . сингонии |
| Низшая | Триклинная Моноклинная Ромбическая | С L2PC 3L23PC |
| Средняя | Тригональная Гексагональная Тетрагональная | L33L23PC L66L27PC L44L25PC |
| Высшая | Кубическая | 4L33L46L29PC |
Внешняя форма кристаллов.Под формой кристаллов понимают совокупность всех его граней. Различают простые формы и комбинации. Если все грани кристаллов неразрывно связаны между собой элементами симметрии, получается простая форма (табл. 4, рис. 20—22).
Довольно часто в одном кристалле могут присутствовать одна, две или несколько простых форм. Закономерное сочетание нескольких простых форм на кристалле называется комбинацией. Сколько видов граней различается на равномерно развитом кристалле, столько простых форм составляют комбинацию.
Внешняя форма кристаллов является важным диагностическим свойством, так как каждому минералу присущи те или иные внешние ограничения. Однако в природных условиях в зависимости от среды, в которой растет кристалл, большинство из них кажутся несимметричными. Для того чтобы обнаружить симметрию кристалла, необходимо замерить его гранные углы.
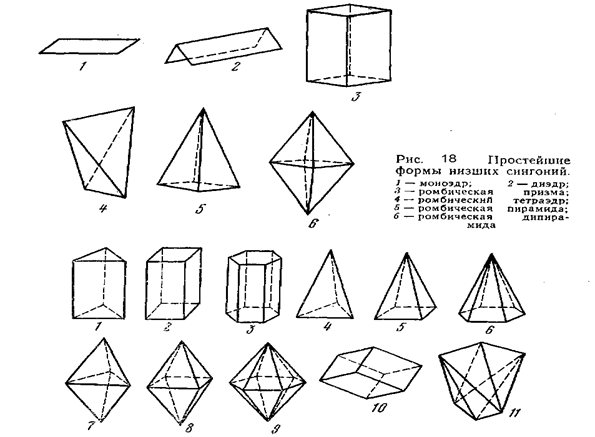
Рис 18. Простейшие формы средних сингоний.
1 - 3 — призмы (1 - тригональная, 2 — тетрагональная, 3 — гексагональная); 4—6 — пирамиды
(4 — тригональная, 5 — тетрагональная, 6 — гексагональная); 7—9 — дипирамиды
(7 — тригональная, 8 — тетрагональная, 9 — гексагональная); 10 — ромбоэдр; 11— скаленоэдр

Рис 19. Простейшие формы высшей сингонии.
1 - тетраэдр; 2 — куб; 3 — октаэдр; 4 — ромбо-додекаэдр; 5 - пентагон-додекаэдр
Простейшие формы кристаллов
| Категория сингонии | Формы кристаллов |
| Низшая | Моноэдр, диэдр, ромбическая призма, ромбический тетраэдр, ромбическая пирамида, ромбическая дипирамида |
| Средняя | Призмы: гексагональные, тетрагональные, тригональные; пирамиды и бипирамнды; гексагональные, тетрагональные, тригональные; ромбоэдр и др. |
| Высшая | Куб, октаэдр, тетраэдр, ромбо-додекаэдр, пентагон-доде каэдр и др. |
 Рис 20. Образование комбинации простых форм у кристалла циркона.
Рис 20. Образование комбинации простых форм у кристалла циркона.
а — тетрагональная призма;
р - тетрагональная дипирамида
Большая часть минералов, распространенных в земной коре, обладает кристаллическим строением. Базируясь на основах кристаллографии, минералогия изучает внешнюю форму минеральных индивидов (кристаллов), их зарождение, рост и закономерности срастаний.
Дата добавления: 2022-02-05; просмотров: 782;











