Понятие о логической функции
В математической логике основными понятиями являются логическая переменная и логическая функция.
Логическими переменными называются знаки (символы), которые принимают различные значения из соответствующей области. Такие переменные будем обозначать, например, буквами латинского алфавита: x1, x2, ..., xi, или y1,y2, ..., yi, или z1, z2, ..., zk. Область значений переменных может быть различной: нуль и единица {0,1}; нуль, плюс единица и минус единица {0,+1,-1}; нуль, единица, два {0,1,2} и др. Если область значений логических переменных содержит два значения, то такие логические переменные называют двоичными или булевыми, если же она содержит три значения, то их называют троичными, а если она содержит четыре более значений, то их называют многозначными переменными. Будем рассматривать только двоичные (булевы) переменные и под выражением “двоичные переменные” будем понимать логические двоичные переменные.
Совокупности значений переменных образуют наборы значений переменных, или просто наборы. Наборы значений логических переменных можно представить в виде двоичных чисел или в виде эквивалентов двоичных чисел. Например, переменные x1, x2, x3, x4 в зависимости от принимаемых значений образуют наборы: 0000, 0001, 0010,0011,0100,0101,0110,0111,1000, ...,1111.
В общем виде набор значений переменных запишем как
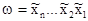 ,
,
где  (j=1,2, ...,n) обозначает конкретное значение переменой xj и равно либо 0, либо 1. Если каждая переменная принимает два значения, а число переменных равно n, то число различных наборов равно 2n . Переменные и наборы играют важную роль в понятии “логическая функция”.
(j=1,2, ...,n) обозначает конкретное значение переменой xj и равно либо 0, либо 1. Если каждая переменная принимает два значения, а число переменных равно n, то число различных наборов равно 2n . Переменные и наборы играют важную роль в понятии “логическая функция”.
Логической функцией называют функцию, зависящую от логических переменных и принимающую значения из того же множества, что и переменные, от которых она зависит. Логические функции двоичных (булевых) переменных принимают одно из двух значений: либо 0, либо 1.
Для обозначения логических функций будем пользоваться записями вида f(x), f(xn, xn-1, ..., x2, x1), yi(x), z(x), u(x) и другими, где в скобках указываются переменные, от которых зависит логическая функция.
Различные значения переменных логической функции образуют наборы значений этой функции. Наборы значений переменных зависят от порядка расположения переменных, поэтому для однозначного задания наборов введем порядок размещения переменных в наборе. Если не оговорено особо, переменные в наборе будем располагать справа налево в порядке возрастания индексов переменных. Например, набор wi =1101 означает, что переменных в наборе четыре и переменные x1=1, x2=0, x3= x4=1.
Совокупность наборов, на которых определена логическая функция, образует область отправления (задания) этой функции. Для логической функции от n переменных эта область содержит 2 различных наборов. Множество значений, на которых определена логическая функция, образует область прибытия. Область прибытия булевых функций содержит два значения: “0” и “1”.
Определим число различных логических функций от n переменных. Из n переменных можно образовать 2n различных наборов.
На каждом наборе логическая функция может принимать значение либо 0, либо 1 независимо от ее значения на других наборах. Отсюда число различных логических функций определяется как произведение 2n чисел 2, т.е. N=22 n (таблица 2.1).
Таблица 2.1
Таблица соответствия логических функций, зависящих от n переменных
| № | Набор значений | Логическая функция | ||||||
| п/п | переменных | ... | ... | |||||
| 00...0 | ||||||||
| 00...1 | ||||||||
| 0...10 | ||||||||
| 0...11 | ||||||||
| ... | ||||||||
| 2n | 1...11 |
Число различных логических функций возрастает с увеличением числа переменных и уже для функций пяти переменных составит огромное число - 4 294 966 296.
Всякая функция от меньшего числа переменных автоматически входит в число функций от большего числа переменных. Логическая функция f(xn, ..., x2,x1,) существенно зависит от переменной xi, если имеет место соотношение
f(xn, ..., xi+1, 0, xi-1, ..., x1)¹f(xn, ..., xi+1, 1, xi-1, ..., x1,).
В противном случае говорят, что функция f(xn, ..., x2,x1,) не зависит существенно от переменной xi, т.е. xi есть фиктивная переменная.
Функции n переменных, которые существенно зависят от всех переменных, называются невырожденными функциями от n переменных. Функции n переменных, которые фактически зависят от меньшего числа переменных, называются вырожденными.
Наборы переменных, на которых логическая функция принимает значение 1, будем называть единичными наборами, а наборы на которых функция принимает значение 0, будем называть нулевыми наборами.
Наряду с функциями, значения которых определены на всех 2n наборах, нередко возникает необходимость рассмотрения функций, значения которых определены только для части наборов. Наборы переменных, на которых значение функции не определено, будем называть неопределенными наборами. Логические функции, значения которых определены только на части наборов переменных, будем называть неполностью определенными функциями. Значения функций на условных наборах могут выбираться произвольным образом. В связи с этим неполностью определенную логическую функцию можно рассматривать как семейство полностью определенных логических функций, отличающихся друг от друга значениями на условных наборах. Если логическая функция содержит k условных наборов, то ей соответствует семейство, состоящее из 2k различных полностью определенных функций, рабочие и запрещенные наборы которых полностью совпадают.
Дата добавления: 2022-02-05; просмотров: 411;











