Методы обнаружения тупика по наличию замкнутой цепочки запросов

Структура графа обеспечивает простое необходимое (но не достаточное) условие для тупика. Для любого графа G =<Х, Е> и вершины х Î Х пусть Р(х) обозначает множество вершин, достижимых из вершины х, то есть

Р(х) = { у½(х, у) Î Е } È { z½(у, z) Î Е & у Î Р(х)}.

Можно сказать, что в ориентированном графе потомством вершины х, которое мы обозначаем как Р(х), называется множество всех вершин, в которые ведут пути из х.

Тогда если существует некоторая вершина х Î Х : х Î Р(х), то в графе G имеется цикл.

Теорема 1. Цикл в графе повторно используемых ресурсов является необходимым условием тупика.

Для доказательства этой теоремы (которое мы опустим, указав, что при желании его можно найти в работе [45]) можно воспользоваться следующим свойст­вом ориентированных графов: если ориентированный граф не содержит цикла, то существует линейное упорядочение вершин, такое, что если существует путь от вершины i к вершине j, то i появляется перед j в этом упорядочении.

Теорема 2. Если S не является состоянием тупика и S 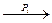S_T, где S_T есть состояние тупика в том и только в том случае, когда операция процесса Р_i есть за­прос и Р_i находится в тупике в S_T.

Это следует понимать таким образом, что тупик может быть вызван только при запросе, который не удовлетворён немедленно. Учитывая эту теорему, можно сделать вывод, что проверка на тупиковое состояние может быть выполнена бо­лее эффективно, если она проводится непрерывно, то есть по мере развития про­цессов. Тогда надо применять редукцию графа только после запроса от некото­рого процесса Р_i и на любой стадии необходимо сначала попытаться сократить с помощью процесса Р_i Если процесс Р_i смог провести сокращение графа, то ника­кие дальнейшие сокращения не являются необходимыми.

Ограничения, накладываемые на распределители, на число ресурсов, запрошен­ных одновременно, и количество единиц ресурсов, приводят к более простым ус­ловиям для тупика.

Пучок (или узел) в ориентированном графе G = <Х, Е> – это подмножество вершин Z Í X, таких что " х Î Z, Р(х) = Z, то есть потомством каждой вершины из Z является само множество Z. Каждая вершина в узле достижима из каждой другой вершины этого узла, и узел есть максимальное подмножество с этим свойством.
Поясним сказанное рис. 7.12.

Рис. 7.12. Пример узла на модели Холта

Следует заметить, что наличие цикла – это необходимое, но не достаточное условие для узла. Так, на рис.7.13 изображены два подграфа. Подграф а представляет собой пучок (узел), тогда как подграф б представляет собой цикл, но узлом не является. В узел должны входить дуги, но они не должны из него выхо­дить.

Рис. 7.13. Узел и цикл в ориентированном графе

Если состояние системы таково, что удовлетворены все запросы, которые могут быть удовлетворены, то существует простое достаточное условие существования тупика. Эта ситуация возникает, если распределители ресурсов не откладывают запросы, которые могут быть удовлетворены, а выполняют их по возможности немедленно (большинство распределителей следует этой дисциплине).

Состояние называется фиксированным, если каждый процесс, выдавший запрос, заблокирован.

Теорема 3. Если состояние системы фиксированное (все процессы, имеющие за­просы, удовлетворены), то наличие узла в соответствующем графе повторно используемых ресурсов является достаточным условием тупика.

Доказательство. Предположим, что граф содержит узел Z. Тогда все процессы в этом узле должны быть заблокированы только по ресурсам, принадлежащимZ,так как никакие ребра не могут выходить из Z по определению. Аналогично, по той же самой причине все распределенные ресурсы узла Z принадлежат процес­сам из Z. Наконец, все процессы в Z должны быть заблокированы согласно усло­вию фиксированности и определению узла. Следовательно, все процессы в узле Z должны быть в тупике.

Допустим, что каждый ресурс имеет единичную ёмкость (по одной единице ре­сурса), то есть |R_j| = 1, (i = 1, 2, ..., m). При этом ограничении наличие цикла также становится достаточным условием тупика.

Теорема 4. Граф повторно используемых ресурсов с единичной ёмкостью указы­вает на состояние тупика тогда и только тогда, когда он содержит цикл.

Доказательство. Необходимость цикла доказывает теорема 1. Для доказательст­ва достаточности допустим, что граф содержит цикл, и рассмотрим только лишь процессы и ресурсы, принадлежащие циклу. Так как каждая вершина–процесс должна иметь входящее и исходящее ребро, она должна иметь выданный запрос на некоторый ресурс, принадлежащий циклу, и должна удерживать некоторый ресурс, принадлежащий тому же циклу. Аналогично, каждый ресурс единичной ёмкости в цикле должен быть захвачен некоторым процессом. Следовательно, каждый процесс в цикле блокируется на ресурсе, который может быть освобож­дён только некоторым процессом из этого цикла; поэтому процессы в цикле на­ходятся в тупике.

Чтобы обнаружить тупик в случае ресурса единичной ёмкости, мы должны про­сто проверить граф повторно используемых ресурсов на наличие циклов.