Модель пространства состояний системы
Приведём еще одну формальную модель (она подробно рассмотрена в работе [92]). Эта модель очень проста, однако она позволяет сформулировать, что нам нужно делать, чтобы не попасть в тупиковое состояние.
Пусть состояние операционной системы будет сводиться к состоянию различных ресурсов в системе (свободны они или кому-то распределены). Состояние системы изменяется процессами, когда они запрашивают, приобретают или освобождают ресурсы; это будут единственно возможные действия (точнее, мы принимаем во внимание только такие действия). Если процесс не блокирован в данном состоянии, он может изменить это состояние на новое. Однако, так как в общем случае невозможно знать заранее, какой путь может избрать произвольный процесс в своей программе (это неразрешимая проблема!), то новое состояние может быть любым из конечного числа возможных. Следовательно, процессы нами будут трактоваться как недетерминированные объекты. Введённые ограничения на известные понятия приводят нас к следующим формальным определениям:
¨ Система есть пара <s, p>, где
s – множество состояний системы {S1, S2, S3, ... , Sn};
p – множество процессов {P1, Р2, Р3, ... , Рk}.
¨ Процесс Рi есть частичная функция, отображающая состояние системы в непустые подмножества её же состояний. Это обозначается так:
Pi: s®{s}
Если Pi определён на состоянии S, то область значений Рi , обозначается как Pi(S). Если Sk Î Pi(Se), то мы говорим, что Pi может изменить состояние Se в состояние Sk посредством операции, и используем обозначение Se 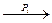 Sk .
Sk .
Наконец, запись Se Sw обозначает, что
Se = Sw или
Se 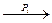 Sw для некоторого i или
Sw для некоторого i или
Se 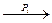 Sk для некоторого i и Sk, и Sk
Sk для некоторого i и Sk, и Sk  Sw.
Sw.
Другими словами, система может быть переведена посредством п ³ 0 операций с помощью т ³0 различных процессов из состояния Se в состояние Sw.
Мы говорим, что процесс заблокирован в данном состоянии, если он не может изменить состояние, то есть в этом состоянии процесс не может ни затребовать, ни получать, ни освобождать ресурсы. Поэтому справедливо будет записать следующее:
¨ Процесс Pi заблокирован в состоянии Se, если не существует ни одного состояния Sk, такого что Se 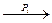 Sk (Pi(Se) = Æ).
Sk (Pi(Se) = Æ).
Далее, мы говорим, что процесс находится в тупике в данном состоянии Se, если он заблокирован в состоянии Se и если вне зависимости от того, какие операции (изменения состояний) произойдут в будущем, процесс остается заблокированным. Поэтому дадим еще одно определение:
¨ Процесс Pi находится в тупике в состоянии Se, если для всех состояний Sk, таких что Se  Sk, процесс Pi блокирован в Sk.
Sk, процесс Pi блокирован в Sk.
Приведём пример. Определим систему <s, p>:
s = {S1, S2, S3, S4}; p = {P1, Р2};
P1(S1) = {S2, S3}; P2(Sl) = {S3};
Pl(S2) = Æ ; P2(S2) = {S1, S4};
Pl(S3) = {S4}; P2(S3) = Æ;
P1(S4) = {S3}; P2(S4) = Æ.
Некоторые возможные последовательности изменений для этой системы таковы:
S1 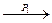 S3; S2
S3; S2 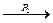 S4; S1
S4; S1  S4.
S4.
Последовательность S1  S4 может быть реализована, например, следующим образом: S1
S4 может быть реализована, например, следующим образом: S1 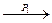 S2; S2
S2; S2 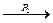 S4 или же S1
S4 или же S1 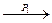 S3; S3
S3; S3 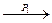 S4.
S4.
Заметим, что процесс Р2 находится в тупике как в состоянии S3, так и в состоянии S4; для последнего случая S2 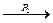 S4 или S2
S4 или S2 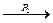 S1 и процесс P1 не становится заблокированным ни в S4, ни в S1.
S1 и процесс P1 не становится заблокированным ни в S4, ни в S1.
 |
Диаграмма переходов этой системы изображена на рис. 7.9.
Рис. 7.9. Пример системы <s, p> на 4 состояния
¨ Состояние S называется тупиковым, если существует процесс Рi, находящийся в тупике в состоянии S.
Теперь мы можем сказать, что тупик предотвращается, по определению, при введении такого ограничения на систему, чтобы каждое её возможное состояние не было тупиковым состоянием.
Введем еще одно определение.
¨ Состояние Si есть безопасное состояние, если для всех Sk, таких что
Si  Sk, Sk не является тупиковым состоянием.
Sk, Sk не является тупиковым состоянием.
Рассмотрим ещё один пример системы <s, p>. Граф её состояний приведен на рис. 7.10. Здесь состояния S2 и S3 являются безопасными; из них система никогда не сможет попасть в тупиковое состояние. Состояния S1 и S4 могут привести как к безопасным состояниям, так и к опасному состоянию S5. Состояние S6 и S7 является тупиковым.

Рис. 7.10. Пример системы <s, p> с безопасными, опасными и тупиковым
состояниями
Наконец, в качестве ещё одной простейшей системы вида <s, p> приведём пример тупика с SR-ресурсами, уже рассмотренный нами в этой главе ранее. Определим следующим образом состояния процессов P1 и Р2, которые используют ресурсы R1 и R2.
Таблица 7.1. Состояния процессов Р1 и Р2
| Состояния для процесса Р1 | Состояния для процесса Р2 | ||
| Не содержит никаких ресурсов | Не содержит никаких ресурсов | ||
| Запросил ресурс R2, не держит никаких ресурсов | Запросил ресурс R1, не держит никаких ресурсов | ||
| Держит ресурс R2 | Держит ресурс R1 | ||
| Запросил ресурс R1, держит ресурс R2 | Запросил ресурс R2, держит ресурс R1 | ||
| Держит ресурсы R1 и R2 | Держит ресурсы R1 и R2 | ||
| Держит ресурс R2 после освобождения ресурса R1 | Держит ресурс R2 после освобождения ресурса R1 |
Пусть состояние системы Sij означает, что процесс P1 находится в состоянии Si, а процесс Р2 – в состоянии Sj. Возможные изменения в пространстве состояний этой системы изображены на рис.7.11. «Вертикальными» стрелками показаны возможные переходы из одного состояния в другое для процесса P1, а «горизонтальными» – для процесса Р2. В данной системе имеются три опасных состояния. Попав в любое из них, мы неминуемо перейдем в тупиковое состояние.
 |
Рис. 7.11. Пример системы
Теперь, когда мы знаем понятия надежного, опасного и безопасного состояний, можно рассмотреть и методы борьбы с тупиками.
Дата добавления: 2022-02-05; просмотров: 552;











