Алгоритм на псевдокоде
Сортировка части массива (L,R)
DO (есть хотя бы 2 элемента, т.е. L<R)
<разделение> (как в 1 версии)
IF (левая часть длиннее правой, т.е.j-L>R-i)
Сортировка части массива (i,R)
R:=j
Else
Сортировка части массива (L,j)
L:=i;
FI
OD
4.4 Варианты заданий
1. Разработать процедуру сортировки массива целых чисел методом пирамидальной сортировки (язык программирования Паскаль или Си). Правильность сортировки проверить путем подсчета контрольной суммы и числа серий в массиве. Предусмотреть подсчет количества пересылок и сравнений (М и С), сравнить их с теоретическими оценками.
2. Разработать процедуру сортировки массива целых чисел методом Хоара (язык программирования Паскаль или Си). Правильность сортировки проверить путем подсчета контрольной суммы и числа серий в массиве. Предусмотреть подсчет количества пересылок и сравнений (М и С), сравнить их с теоретическими оценками.
3.Сравнить метод пирамидальной сортировки и метод Хоара по количеству сравнений и пересылок для различных типов массивов. Разработать процедуру построения графика зависимости М+С от размера массива n для случайного массива.
4. Сравнить трудоемкости метода Хоара и метода прямого выбора для различных типов массивов. Разработать процедуру построения графика зависимости величин М и С от размера массива
5. Экспериментально определить устойчивость и зависимость от начальной отсортированности массива пирамидальной сортировки и метода Хоара.
6. Опытным путем определить константы в выражениях оценки для количества сравнений и пересылок в методе Хоара.
7. Реализовать метода Хоара с меньшим количеством рекурсивных вызовов. Определить необходимое количество рекурсивных вызовов.
8. Запрограммировать метод Хоара без использования рекурсивных вызовов.
5. Работа с линейными списками
5.1 Указатели. Основные операции с указателями
Каждый элемент данных, хранящихся в памяти компьютера, имеет свой адрес. Адреса могут находиться в специальных переменных, называемых указателями. Мы будем рассматривать типизированные указатели, которые могут хранить адреса только объектов определенного типа.
Пусть указатели р и q содержат адрес объекта x некоторого типа tData. Графически будем изображать это следующим образом:
p
 |
x: tData
q
Рисунок 12 Равенство указателей
Стрелка начинается в указателе и указывает на объект в целом, а не на отдельную компоненту, поэтому указатели p и q равны. Заметим, что обычно адрес объекта совпадает с адресом его первой компоненты. Можно обращаться к переменной по имени, а можно по адресу. При обращении по адресу не нужно знать имени переменной.
Основные операции с указателями приведены в следующей таблице.
Таблица 2 Основные операции с указателями
| Операция | Псевдокод | Комментарии |
| 1. Присваивание | p:=q | Указателю р присвоить значение указателя q |
| 2. Сравнение | p=q, p≠q | Сравнение значений указателей р и q |
| 3. Получение адреса | p:=@x | Указателю р присвоить адрес переменной х |
| 4.Доступ по адресу | *p=y *p=*q | Переменной по адресу р присвоить значение переменной по адресу q |
| 5. Доступ к отдельной компоненте | p→comp:=х | Компоненте comp переменной по адресу р присвоить значение переменной х |
| 6. Отсутствие адреса | NIL | Значение указателя р не равно никакому адресу |
5.2 Основные операции с линейными списками
Списком называется последовательность однотипных элементов, связанных между собой указателями. Будем считать, что элементы списка имеют тип tLE, указатели на элементы списка имеют тип pLE.
X: tLE p: pLE
| Next |
| Data |
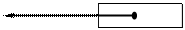 |
Рисунок 13 Указатель на элемент списка
Поле Next является указателем на элемент списка и может занимать произвольное место в структуре элемента. Однако если оно является первым элементом структуры, то его адрес совпадает с адресом элемента списка, и это позволяет оптимизировать многие операции со списками. Поле Data содержит информацию, которая будет учитываться при сортировке.
Рассмотрим два вида списков: стек и очередь. Стек характеризуется тем, что новый элемент добавляется в начало последовательности, а удаляться может только первый элемент списка. При добавлении в очередь новый элемент ставится в конец списка, удаляется первый элемент последовательности.
Рассмотрим основные операции со стеком и очередью. Для работы со стеком необходимо иметь указатель на начало списка. Обозначим его Head. При работе с очередью требуется дополнительный указатель на конец очереди. Обозначим его Tail. Иногда при работе с очередью удобно объединять указатели Head и Tail в виде полей некоторой переменной Queue.
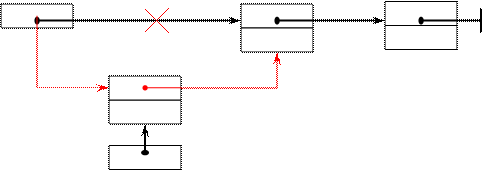
Добавление элемента по адресу р в стек.
Head
 |
2) 1)
p
1) p→Next:=Head
2) Head:=p
Рисунок 14 Добавление в стек
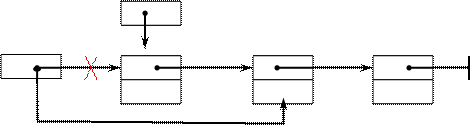
Удаление из стека или очереди (при условии, что список не пуст, т.е. Head≠NIL)
p
 |
Head 1)
2)
1) p:=Head
2) Head:=p→Next
<освободить память по адресу p>
Рисунок 15 Удаление из стека
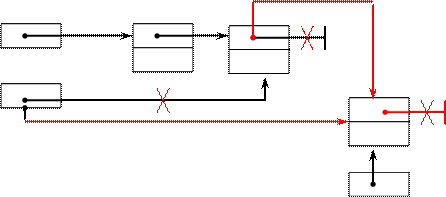
Добавление элемента по адресу р в очередь.
 Head
Head
2)
Tail
1)
3)
p
Рисунок 16 Добавление в очередь
1) p→Next:=NIL
2) IF (Head≠NIL) Tail→Next:=p
ELSE Head:=p
FI
3) Tail:=p
Операцию добавления элемента в очередь можно оптимизировать в случае, если поле Next является первой компонентой элемента очереди и его адрес совпадает с адресом всего элемента. Зададим пустую очередь следующим образом:
Head
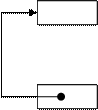 |
Tail:=@Head
Tail
Рисунок 17 Структура очереди
Эту операцию назовем инициализацией очереди. Тогда добавление элемента в очередь будет происходить в два раза быстрее:
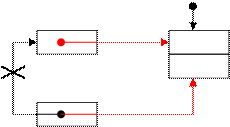 |
Head 1) p
Tail
2)
Рисунок 18 Добавление в очередь
1) Tail->Next:=p
2) Tail:=p
Перемещение элемента из начала списка List в конец очереди Queue.
3)
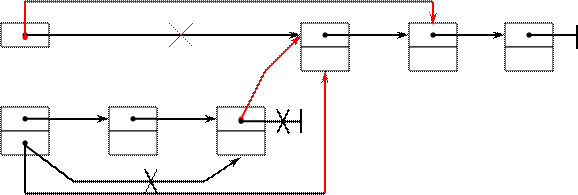
List
1)
Head
Queue
2)
Tail
Рисунок 19 Перемещение элемента
1) Queue.Tail→Next:=List
2) Queue.Tail:=List
3) List:=List→Next
6. Методы сортировки последовательностей
6.1 Метод прямого слияния
В основе метода прямого слияния лежит операция слияния серий. р-серией называется упорядоченная последовательность из р элементов.
Пусть имеются две упорядоченные серии a и b длины q и r соответственно. Необходимо получить упорядоченную последовательность с, которая состоит из элементов серий a и b. Сначала сравниваем первые элементы последовательностей a и b. Минимальный элемент перемещаем в последовательность с. Повторяем действия до тех пор, пока одна из последовательностей a и b не станет пустой, оставшиеся элементы из другой последовательности переносим в последовательность с. В результате получим (q+r)-серию.
Пример.Слить две серии a=(1, 4, 5, 6′) и b=(2, 3, 6″, 7, 8)
Условные обозначения | операция сравнения первых элементов списков.
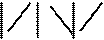 а а
| 6′ | ||||||||
| b | 6″ | ||||||||
| c | 6′ | 6″ |
Рисунок 20 Слияние серий
Дата добавления: 2022-02-05; просмотров: 522;











