Глава 2. Формальные теории.

Одним из основных понятий математической логики является понятие формальной теории или исчисления. Это понятие было первоначально разработано для формализации логики и теории доказательств. Формальная теория является эффективным механизмом получения новых теорем. Кроме того, аппарат формальной теории позволяет решать задачи, связанные с математическим моделированием различных явлений и процессов.

Формальная теория считается заданной, если известны следующие четыре составляющих:

1. Алфавит – конечное или счетное множество символов.

2. Формулы,которые по специальным правилам строятся из символов алфавита. Формулы, как правило, составляют счетное множество.

Алфавит и формулы определяют язык или сигнатуру формальной теории.

3. Аксиомы – выделенное из множества формул специальное подмножество. Множество аксиом может быть конечным или бесконечным. Бесконечное множество аксиом задается с помощью конечного множества схем аксиом и правил порождения конкретных аксиом из схемы аксиом. Различают два вида аксиом: логические (общие для класса формальных теорий) и собственные (определяющие содержание конкретной теории).

4. Правила вывода – множество отношений (как правило, конечное) на множестве формул, позволяющие из аксиом получать теоремы формальной теории.

Обратите внимание, что здесь аксиомы – это необязательно утверждения, не требующие доказательства.

Определение. Выводом формальной теории называется последовательность формул 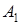, , 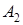…, , 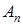в которой все формулы – либо аксиомы, либо получаются из предыдущих по правилам вывода.

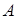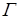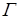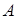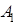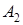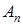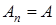Говорят, что формула выводима из множества формул (обозначение: ├ ), если существует вывод , , …, , где , и есть три возможности:

· ;

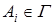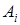· - аксиома;

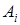· получаются из предыдущих формул по правилам вывода.

Формулы из множества 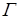называются посылками или гипотезами вывода.

Примеры выводов мы рассмотрим в определенных формальных теориях.

В частном случае, когда 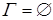, имеет место обозначение: ├ 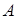, и формула 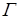называется выводимой в данной теории (или теоремой данной теории). Иногда значок ├ записывается так: ├ 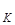, где 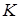– обозначение данной теории.

В Содержание.