Отношения логической эквивалентности и логического следствия.
Определение. Формулы 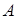 и
и 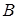 называются логически эквивалентными тогда и только тогда, когда формула
называются логически эквивалентными тогда и только тогда, когда формула 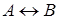 – тавтология.
– тавтология.
Замечание. Формула 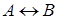 – тавтология, если таблицы истинности формул
– тавтология, если таблицы истинности формул 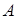 и
и 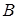 совпадают.
совпадают.
Пример. По законам де Моргана, логически эквивалентны формулы 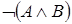 и
и 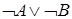 , а также формулы
, а также формулы 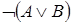 и
и  .
.
Теорема. Отношение логической эквивалентности является отношением эквивалентности.
Рефлексивность, симметричность и транзитивность данного отношения следуют из замечания.
Справедливы правило подстановки и правило замены.
Пусть 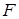 и
и 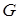 – формулы, содержащие букву
– формулы, содержащие букву 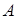 ,
, 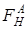 и
и 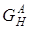 – формулы, полученные из формул
– формулы, полученные из формул 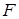 и
и 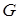 соответственно подстановкой вместо буквы
соответственно подстановкой вместо буквы 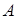 формулы
формулы 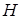 .
.
Правило подстановки.Если формула 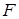 логически эквивалентна формуле
логически эквивалентна формуле 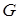 , то формула
, то формула 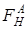 логически эквивалентна формуле
логически эквивалентна формуле 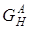 .
.
Пусть 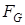 – формула, в которой выделена некоторая подформула
– формула, в которой выделена некоторая подформула 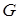 ,
,  – формула, полученная из формулы
– формула, полученная из формулы 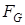 заменой
заменой 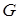 на некоторую формулу
на некоторую формулу 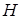 .
.
Правило замены.Если формулы 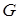 и
и 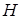 логически эквивалентны, то логически эквивалентны и формулы
логически эквивалентны, то логически эквивалентны и формулы 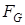 и
и  .
.
Доказательства правил подстановки и замены основано на сравнении таблиц истинности соответствующих формул.
Пример.Известна тавтология  (проверьте самостоятельно). По правилу подстановки, формула
(проверьте самостоятельно). По правилу подстановки, формула 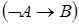 логически эквивалентна формуле
логически эквивалентна формуле 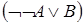 . По правилу замены, примененному к закону двойного отрицания, получаем, что формула
. По правилу замены, примененному к закону двойного отрицания, получаем, что формула 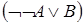 логически эквивалентна формуле
логически эквивалентна формуле 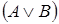 . Следовательно, по свойству транзитивности, формулы
. Следовательно, по свойству транзитивности, формулы 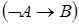 и
и 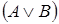 логически эквивалентны.
логически эквивалентны.
Определение. Говорят, что формула 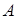 логически влечет формулу
логически влечет формулу 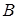 (из формулы
(из формулы 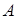 логически следует формула
логически следует формула 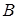 ), если формула
), если формула 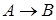 является тавтологией.
является тавтологией.
Теорема. Отношение логического следствия является отношением предпорядка, то есть рефлексивным и транзитивным отношением.
Пример.Формула 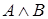 логически влечет формулу
логически влечет формулу 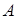 . В самом деле, в примере 1 предыдущего пункта было доказано, что формула
. В самом деле, в примере 1 предыдущего пункта было доказано, что формула 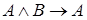 является тавтологией.
является тавтологией.
В Содержание.
Задачи.
1. Установить, является ли предложение высказыванием, и если является, истинно оно или ложно.
1) Волга впадает в Каспийское море.
2) Студент второго курса.
3) 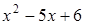 .
.
4)  .
.
5) Существует человек, который не старше своего отца.
6) 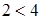 .
.
7) Марс есть спутник Земли.
8) 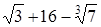 .
.
9) 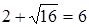 .
.
10) Который час?
2. Установить, является ли предложение высказыванием, и если является, истинно оно или ложно.
1)  .
.
2) 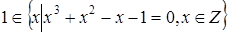 .
.
3) 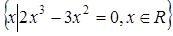 .
.
4) 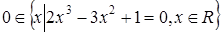 .
.
5) 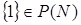 .
.
6) 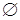 .
.
7) 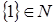 .
.
8) 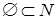 .
.
9) 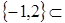
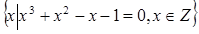 .
.
10) 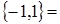
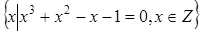 .
.
3. Среди следующих высказываний выделить элементарные и составные. В составных высказываниях обозначить элементарные высказывания буквами и записать с помощью логических символов.
1) Число 6 является делителем числа 36.
2) Число 225 делится нацело на 5.
3) Число 225 делится нацело на 5 и не делится на 10.
4) Если 81 делится нацело на 9, то 81 делится на 3.
5) 16 кратно 2.
6) 18 кратно 2 и 3.
7)  .
.
8) Число 39 имеет 2 простых делителя.
9) Двузначное число 19 простое.
10) Корнями уравнения  являются числа 2 и 3.
являются числа 2 и 3.
4. Пусть 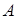 обозначает высказывание “Я увлекаюсь горным туризмом”, а
обозначает высказывание “Я увлекаюсь горным туризмом”, а 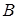 обозначает высказывание “Я изучаю программирование”. Дайте словесную формулировку следующих высказываний:
обозначает высказывание “Я изучаю программирование”. Дайте словесную формулировку следующих высказываний:
1) 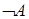 ; 2)
; 2) 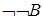 ; 3)
; 3) 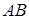 ; 4)
; 4) 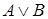 ; 5)
; 5) 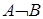 ; 6)
; 6) 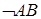 ;
;
7)  ; 8)
; 8) 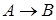 ; 9)
; 9) 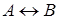 ; 10)
; 10) 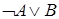 .
.
5. Проверить, является ли формула тавтологией, без построения таблицы истинности.
1) 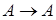 . .
| 6)  . .
|
2) 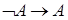 . .
| 7)  . .
|
3) 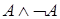 . .
| 8) 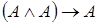 . .
|
4)  . .
| 9) 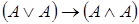 . .
|
5) 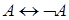 . .
| 10) 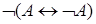 . .
|
6. Доказать, что формула является тавтологией, без построения таблицы истинности. Во всех формулах выделить всевозможные подформулы.
1)  .
.
2) 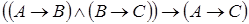 .
.
3) 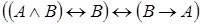 .
.
4) 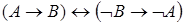 .
.
5) 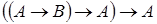 .
.
6) 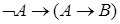 .
.
7) 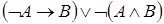 .
.
8)  .
.
9) 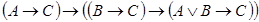 .
.
10) 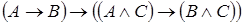 .
.
7. Доказать, что формулы логически эквивалентны.
1) 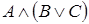 и
и  .
.
2) 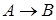 и
и 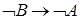 .
.
3)  и
и 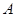 .
.
4) 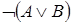 и
и  .
.
5) 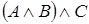 и
и 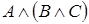 .
.
6) 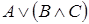 и
и 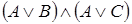 .
.
7) 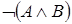 и
и 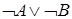 .
.
8)  и
и 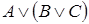 .
.
9) 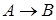 и
и 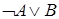 .
.
10) 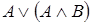 и
и 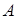 .
.
8. Доказать, что первая формула логически влечет вторую формулу.
1) 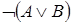 ;
; 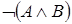 .
.
2) 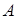 ;
; 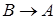 .
.
3) 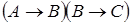 ;
; 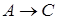 .
.
4) 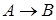 ;
; 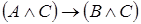 .
.
5) 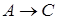 ;
; 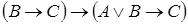 .
.
6) 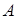 ;
; 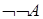 .
.
7) 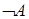 ;
; 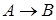 .
.
8) 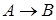 ;
; 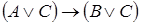 .
.
9) 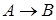 ;
; 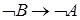 .
.
10) 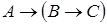 ;
;  .
.
9. Доказать теорему о том, что отношение логической эквивалентности является отношением эквивалентности.
10. Доказать теорему о том, что отношение логического следования является отношением предпорядка.
В Ответы и указания.
В Содержание.
Дата добавления: 2022-02-05; просмотров: 501;











