С активной нагрузкой
Рассмотрим простейший КМДП усилитель с активной нагрузкой в режиме малых входного и выходного сигналов, что позволяет считать его линейной системой. Для анализа усилителя воспользуемся операторным методом. В дальнейшем, если не декларировано другое, все ПЕРЕМЕННЫЕ значения, как аргументов, и функций, по умолчанию предполагаем функциями комплексной переменной 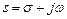 , например,
, например, 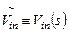 , или
, или 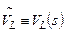 , или
, или 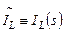 . В целях сокращения размеров формул, для специально оговоренного режима любые напряжения и токи в большинстве случаев будем обозначать как
. В целях сокращения размеров формул, для специально оговоренного режима любые напряжения и токи в большинстве случаев будем обозначать как 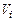 и
и 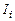 , имея в виду, что
, имея в виду, что 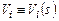 и
и 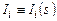 . (3.7)
. (3.7)
Вначале сделаем следующее замечание. Выражения (3.1) и (3.2), иллюстрирующие ток в транзисторе в режиме малого сигнала, как линейную суперпозицию постоянного режимного тока 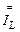 и переменного малого тока
и переменного малого тока 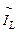 , также иллюстрируют концепцию, упрощающую анализ таких схем. Согласно концепции малого сигнала, i-й транзистор, как нелинейный источник тока, зависящий от входного напряжения, состоит из двух параллельных независимых источников тока. В первом протекает постоянный режимный ток
, также иллюстрируют концепцию, упрощающую анализ таких схем. Согласно концепции малого сигнала, i-й транзистор, как нелинейный источник тока, зависящий от входного напряжения, состоит из двух параллельных независимых источников тока. В первом протекает постоянный режимный ток 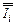 , а во втором – малый переменный ток
, а во втором – малый переменный ток 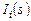 . Соответственно схема из таких транзисторов разделяется на две независимые эквивалентные схемы.
. Соответственно схема из таких транзисторов разделяется на две независимые эквивалентные схемы.
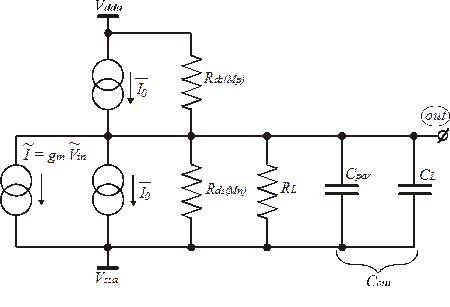
Рис. 3.6. Эквивалентная схема простейшего КМДП усилителя с активной нагрузкой в режиме малого сигнала.
В первой представлены режимные токи 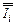 и режимные потенциалы
и режимные потенциалы 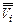 , а с помощью второй производится анализ прохождения в линейной системе переменного малого сигнала, т.е. расчет переменных токов
, а с помощью второй производится анализ прохождения в линейной системе переменного малого сигнала, т.е. расчет переменных токов 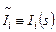 и потенциалов
и потенциалов 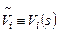 . Подобная концепция применима для любой нелинейной системы, цепи которой работают в режиме малого сигнала.
. Подобная концепция применима для любой нелинейной системы, цепи которой работают в режиме малого сигнала.
С учетом сказанного в предыдущем абзаце, на рис. 3.6 изображена эквивалентная схема усилителя на рис. 3.3.
В эквивалентной схеме на рис. 3.6 каждый транзистор представлен в виде двух источников тока, режимного и сигнального. То же относится и к узловым потенциалам. Уравнение Кирхгофа для этой схемы имеет вид:
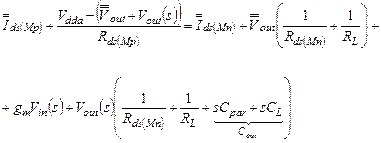 (3.8)
(3.8)
Нас интересует стационарный случай, при котором все переходные процессы уже завершены, и режимные потенциалы (постоянные составляющие потенциалов) во всех узлах неизменны. В этом случае закон Кирхгофа выполняется как для постоянных составляющих, так и для переменных составляющих всех токов в отдельности. Соответственно запишем два уравнения Кирхгофа для обеих составляющих.
Для постоянной составляющей:
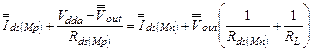 (3.9)
(3.9)
Методам обеспечения равенства обеих частей выражения (3.9) ниже посвящен достаточно большой объем настоящего пособия.
Для переменной составляющей:
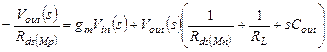 (3.10)
(3.10)
Эквивалентная схема, соответствующая уравнению (3.10) для переменной составляющей, приведена на рис. 3.7(a).
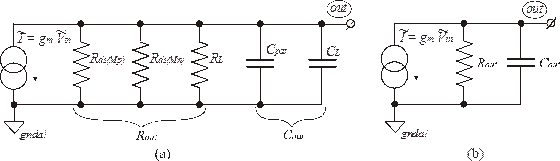
Рис. 3.7. Малосигнальные эквивалентные схемы простейшего усилителя с активной нагрузкой: (а) полная малосигнальная эквивалентная схема соответствующая уравнению (3.10); (b) упрощенная эквивалентная схема, соответствующая уравнениям (3.11) и (3.12).
Из рассмотрения уравнения (3.10) и рисунка 3.7(a) следует правило построения эквивалентной схемы для переменной составляющей:
· на схеме отсутствуют источники постоянного тока (это, конечно, очевидное положение);
· все источники постоянного напряжения заменяются узлами с нулевыми потенциалами.
Из уравнения (3.10) выводится передаточная функция простейшего усилителя:
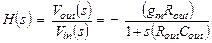 (3.11)
(3.11)
Здесь 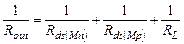 (3.12)
(3.12)
Упрощенная эквивалентная схема, соответствующая уравнениям (3.11) и (3.12) для переменной составляющей, приведена на рис. 3.7(b).
Поскольку рассматривается стационарный случай, то в выражении 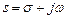 параметр
параметр 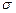 равен нулю,
равен нулю, 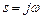 , и комплексная передаточная функция (3.11) содержит информацию и об амплитудночастотной характеристике (АЧХ), и о фазочастотной характеристике (ФЧХ) усилителя:
, и комплексная передаточная функция (3.11) содержит информацию и об амплитудночастотной характеристике (АЧХ), и о фазочастотной характеристике (ФЧХ) усилителя:
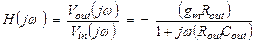 (3.13)
(3.13)
Из (3.12) легко вывести выражения для модуля и фазы 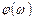 передаточной функции:
передаточной функции:
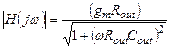 ;
;  (3.14)
(3.14)
Очевидно, что параметр 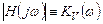 представляет собой коэффициент усиления усилителя, зависящий от частоты согласно выражению (3.14).
представляет собой коэффициент усиления усилителя, зависящий от частоты согласно выражению (3.14).
На малых частотах, при которых круговая частота сигнала много меньше собственной круговой частоты полюса передаточной функции, т.е. 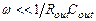 , выражение для
, выражение для 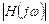 значительно упрощается:
значительно упрощается:
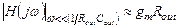 (3.15)
(3.15)
На высоких частотах, при которых круговая частота сигнала много больше собственной круговой частоты полюса передаточной функции, т.е. 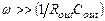 , выражение для
, выражение для 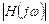 также упрощается и имеет вид:
также упрощается и имеет вид:
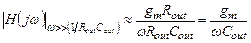 (3.16)
(3.16)
Зависимости от частоты для 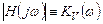 , как точные, согласно (3.14), так и приближенные, согласно (3.15) и (3.16), представлены в логарифмических координатах на рисунке 3.8. Там же представлена частотная зависимость фазы
, как точные, согласно (3.14), так и приближенные, согласно (3.15) и (3.16), представлены в логарифмических координатах на рисунке 3.8. Там же представлена частотная зависимость фазы 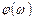 . Как модуль, так и фаза передаточной функции усилительного каскада почти идентичны последним для пассивной интегрирующей RC цепи; отличие состоит в наличии в передаточной функции усилителя дополнительного коэффициента
. Как модуль, так и фаза передаточной функции усилительного каскада почти идентичны последним для пассивной интегрирующей RC цепи; отличие состоит в наличии в передаточной функции усилителя дополнительного коэффициента 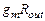 , представляющего значение усиления.
, представляющего значение усиления.
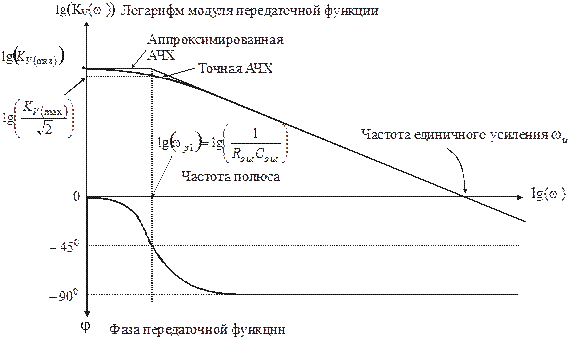
Рис. 3.8. Зависимости от частоты в логарифмических координатах для простейшего усилителя коэффициента усиления 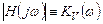 и фазы
и фазы 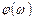 .
.
Отметим, что рассматриваемый усилитель является однокаскадным, поскольку «узкое», но очевидное, определение однокаскадного усилителя включает принцип генерирования переменного тока в выходной цепи именно во входных транзисторах, а, именно, тех, входы которых подключены к входному сигналу.
Параметр 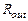 обозначает резистор, номинал которого равен значению сопротивления параллельного соединения обозначенных в этом выражении резисторов. На рис. 3.7(b) изображена упрощенная малосигнальная эквивалентная схема усилителя с учетом такого упрощающего представления.
обозначает резистор, номинал которого равен значению сопротивления параллельного соединения обозначенных в этом выражении резисторов. На рис. 3.7(b) изображена упрощенная малосигнальная эквивалентная схема усилителя с учетом такого упрощающего представления.
Этот рисунок, очевидно, напоминает изображение одного из представлений источника питания, а, именно, в виде источника тока 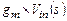 с параллельными ему внутренним резистором и конденсатором нагрузки. Однако, в отличие от стандартного источника питания, резистор
с параллельными ему внутренним резистором и конденсатором нагрузки. Однако, в отличие от стандартного источника питания, резистор 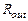 не является внутренним активным сопротивлением источника питания. В рассматриваем случае:
не является внутренним активным сопротивлением источника питания. В рассматриваем случае:
(А) единственный активный резистор 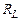 является внешним компонентом, а не внутренней принадлежностью источника тока;
является внешним компонентом, а не внутренней принадлежностью источника тока;
(В) два других заявленных «резистора», 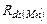 и
и 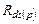 , хотя и являются принадлежностями источников тока, однако, на самом деле, физически не являются резисторами, поскольку представляют результат умозрительной аппроксимации тока МДПТ в пологой области, обосновываемой выражением (3.2) По этой причине «резисторы»
, хотя и являются принадлежностями источников тока, однако, на самом деле, физически не являются резисторами, поскольку представляют результат умозрительной аппроксимации тока МДПТ в пологой области, обосновываемой выражением (3.2) По этой причине «резисторы» 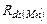 и
и 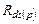 не учитываются при оценке шума усилителя;
не учитываются при оценке шума усилителя;
(С) если рассматриваемый усилитель должен иметь возможно более высокое усиление, то в нем (как и во всех однокаскадных усилителях), в отличие от стандартных источников питания, эквивалентный резистор, параллельный малосигнальному источнику тока, согласно (3.14), (3.15) и (3.16), должен иметь возможно более высокое сопротивление.
Согласно изложенным выше доводам, даже в отсутствие реального резистора нагрузки 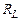 , ВАХ выходного узла усилителя проявляется как ВАХ резистора. Этот эффект, связанный с выходным узлом, позволяет этот эквивалентный резистор назвать выходным резистором, который в выражениях (3.11) – (3.16) был авансом обозначен как
, ВАХ выходного узла усилителя проявляется как ВАХ резистора. Этот эффект, связанный с выходным узлом, позволяет этот эквивалентный резистор назвать выходным резистором, который в выражениях (3.11) – (3.16) был авансом обозначен как 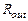 с индексом «out».
с индексом «out».
Как явствует из выражений (3.15) и (3.16), а также видно на рис. 3.8, существуют границы и для коэффициента усиления, и интервала частот, при котором усилитель все еще усиливает, т.е. 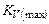 и
и 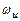 соответственно. Коэффициент усиления максимален, очевидно, при
соответственно. Коэффициент усиления максимален, очевидно, при 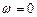 , а при
, а при 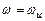 усиление отсутствует, т.е. коэффициент усиления равен единице.
усиление отсутствует, т.е. коэффициент усиления равен единице.
Рассмотрим факторы, увеличивающие как 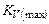 , так и
, так и 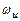 в однокаскадном усилителе.
в однокаскадном усилителе.
Прежде отметим, что присутствие подключенного к выходу резистора 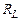 уменьшает значение
уменьшает значение 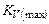 , поэтому однокаскадные усилители с высоким выходным сопротивлением целесообразно применять при подключении к выходу усилителя только конденсаторов. Для подключения к выходу усилителя активного нагрузочного резистора необходимо иметь еще, как минимум, один каскад усиления. На затвор входного транзистора второго каскада поступает сигнал, уже усиленный первым каскадом, поэтому коэффициент усиления многокаскадного усилителя увеличивается пропорционально общему коэффициенту усиления всех каскадов. Однокаскадные же усилители используются почти исключительно с емкостной нагрузкой, а, именно, в схемах с переключаемыми конденсаторами (см. главу I).
, поэтому однокаскадные усилители с высоким выходным сопротивлением целесообразно применять при подключении к выходу усилителя только конденсаторов. Для подключения к выходу усилителя активного нагрузочного резистора необходимо иметь еще, как минимум, один каскад усиления. На затвор входного транзистора второго каскада поступает сигнал, уже усиленный первым каскадом, поэтому коэффициент усиления многокаскадного усилителя увеличивается пропорционально общему коэффициенту усиления всех каскадов. Однокаскадные же усилители используются почти исключительно с емкостной нагрузкой, а, именно, в схемах с переключаемыми конденсаторами (см. главу I).
При отсутствии в однокаскадном усилителе с высоким выходным сопротивлением 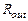 резистивной нагрузки
резистивной нагрузки 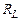 , его максимальный коэффициент усиления
, его максимальный коэффициент усиления 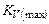 и частота единичного усиления
и частота единичного усиления 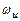 определяются вольтамперными характеристиками транзисторов, работающих в пологом режиме, определяющими параметры
определяются вольтамперными характеристиками транзисторов, работающих в пологом режиме, определяющими параметры 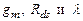 транзисторов, как входного, так и нагрузочного а также емкостью конденсатора нагрузки
транзисторов, как входного, так и нагрузочного а также емкостью конденсатора нагрузки 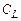 .
.
Ниже приводится выражение для тока 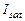 в рамках модели Level1 для МДПТ в пологом режиме, содержащее все перечисленные параметры (см. главу II):
в рамках модели Level1 для МДПТ в пологом режиме, содержащее все перечисленные параметры (см. главу II):
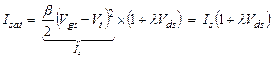 (3.17)
(3.17)
Из (3.17) получают выражения для крутизны по затвору 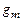 и сопротивления сток-исток
и сопротивления сток-исток 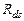 :
:
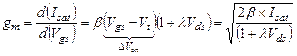 (3.18а)
(3.18а)
В хорошо спроектированном МДП транзисторе даже при минимальной для данной технологии длине затвора 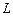 параметр
параметр 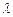 имеет небольшую величину (порядка 0,1 … 0,2), поэтому с достаточной для инженерных оценок степенью точности можно считать:
имеет небольшую величину (порядка 0,1 … 0,2), поэтому с достаточной для инженерных оценок степенью точности можно считать:
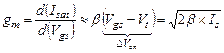 (3.18б)
(3.18б)
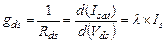 (3.19)
(3.19)
Параметр 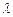 обратно пропорционален длине затвора
обратно пропорционален длине затвора 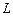 и сопротивлению сток-исток
и сопротивлению сток-исток 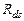 (см главу II), а также зависит от электрофизических свойств подзатворной области, включая толщину и диэлектрическую проницаемость диэлектрика, а также свойств области полупроводника между стоком и истоком (значения и градиента концентрации примеси, проводимости и глубин диффузионных областей, электрических полей и др.).
(см главу II), а также зависит от электрофизических свойств подзатворной области, включая толщину и диэлектрическую проницаемость диэлектрика, а также свойств области полупроводника между стоком и истоком (значения и градиента концентрации примеси, проводимости и глубин диффузионных областей, электрических полей и др.).
Как следует из выражений (3.11) – (3.16), из параметров нагрузочного транзистора в эти выражения входит только его выходное сопротивление 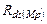 , прямо пропорциональное длине канала (см. главу II). Если предположить, что длины каналов входного и нагрузочного транзисторов резко отличаются, т.е.
, прямо пропорциональное длине канала (см. главу II). Если предположить, что длины каналов входного и нагрузочного транзисторов резко отличаются, т.е. 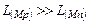 , то выходное сопротивление усилителя
, то выходное сопротивление усилителя 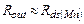 , и с учетом того, что в выражениях (3.11) – (3.16) параметр
, и с учетом того, что в выражениях (3.11) – (3.16) параметр 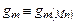 выражение для максимального коэффициента принимает вид:
выражение для максимального коэффициента принимает вид:
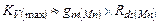 (3.20)
(3.20)
Произведение 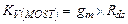 является одним из главных параметров транзистора и называется собственным коэффициентом усиления по напряжению транзистора. Высокое значение
является одним из главных параметров транзистора и называется собственным коэффициентом усиления по напряжению транзистора. Высокое значение 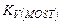 обеспечивает как высокий коэффициент усиления в усилителе, так и низкие утечки в разомкнутых МДП ключах.
обеспечивает как высокий коэффициент усиления в усилителе, так и низкие утечки в разомкнутых МДП ключах.
Разумеется, варьируя размерами нагрузочного транзистора, возможно достижение в простейшем усилителе значения 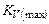 , близкого к значению собственного коэффициента усиления входного транзистора, но выигрыш в величине
, близкого к значению собственного коэффициента усиления входного транзистора, но выигрыш в величине 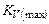 при этом будет не более, чем в 2 раза, а значение
при этом будет не более, чем в 2 раза, а значение 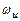 в некоторых случаях (при относительно небольших значениях
в некоторых случаях (при относительно небольших значениях 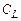 ) может довольно значительно уменьшиться. Дело в том, что значение
) может довольно значительно уменьшиться. Дело в том, что значение 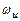 обратно пропорционально величине
обратно пропорционально величине 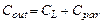 (см. ниже), а увеличение длины затвора нагрузочного транзистора влечет пропорциональное увеличение его ширины и, следовательно, к увеличению вклада паразитной емкости
(см. ниже), а увеличение длины затвора нагрузочного транзистора влечет пропорциональное увеличение его ширины и, следовательно, к увеличению вклада паразитной емкости 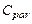 в общую емкость
в общую емкость 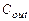 на выходе усилителя.
на выходе усилителя.
Согласно (3.18) и (3.19), выражение для собственного коэффициента усиления транзистора представляется в виде:
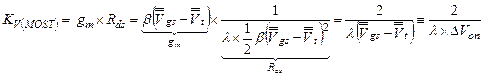 (3.21)
(3.21)
При 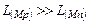 и, следовательно,
и, следовательно, 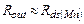 , характеристики усилителя с активной нагрузкой близки к характеристикам такого же усилителя, но в котором источником тока является не транзистор, а идеальный источник тока. Нагрузочным конденсатором является
, характеристики усилителя с активной нагрузкой близки к характеристикам такого же усилителя, но в котором источником тока является не транзистор, а идеальный источник тока. Нагрузочным конденсатором является 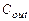 . В таком усилителе малосигнальные характеристики не зависят от нагрузочного транзистора, и становится возможным определить вклад в характеристики усилителя как входного транзистора, так и нагрузочного, в отдельности. В дальнейшем подобный прием будет применяться достаточно часто.
. В таком усилителе малосигнальные характеристики не зависят от нагрузочного транзистора, и становится возможным определить вклад в характеристики усилителя как входного транзистора, так и нагрузочного, в отдельности. В дальнейшем подобный прием будет применяться достаточно часто.
Предположим, что характеристики нагрузочного транзистора близки к характеристикам входного, а, именно, 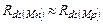 и
и 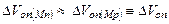 . В этом случае оценка максимального коэффициента усиления
. В этом случае оценка максимального коэффициента усиления 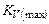 очень проста, поскольку
очень проста, поскольку 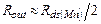 , и, очевидно,
, и, очевидно,
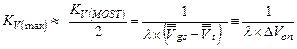 (3.22)
(3.22)
Дата добавления: 2022-02-05; просмотров: 516;











