Эффективная масса электрона

Взаимодействие электронов с кристаллической решеткой столь сложно, что непосредственный учет этого взаимодействия представляет серьезные трудности. Однако, их можно обойти, если ввести так называемую эффективную массу электрона m*.

Приписывая электрону, находящемуся в кристалле массу m*, можно считать его свободным. В этом случае можно описывать его движение в кристалле аналогично движению свободного электрона. Разница между m* и m обусловлена взаимодействием электрона с периодическим полем кристаллической решетки. Приписывая электрону эффективную массу, мы учитываем это взаимодействие.

Проведем графо-аналитический анализ поведения электрона в пределах нечетной разрешенной энергетической зоны для одномерного кристалла.

На рис. приведена дисперсионная зависимость (Е=f(k)) для электрона. В рассматриваемом случае она может быть представлена функцией, подобной 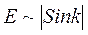. На рис. показана зависимость скорости электрона от волнового числа (v~dE/dk). Ее график легко построить, если вспомнить геометрический смысл первой производной. В точках -p/а, 0, p/а скорость v= 0. В точках - p/2а и p/2а скорость максимальна и в первом случае v<0 во втором v>0. Получаем график v~dE/dk, подобный отрезку синусоиды. График на рис w ~ d²E/dk² строится аналогично, поскольку представляет собой первую производную от графика на рис.

Теперь график на рис., который отображает эффективную массу электрона:

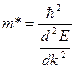При k = 0 величина d²E/dk² максимальна и положительна, поэтому эффективная масса m* минимальна и >0. При увеличении абсолютного значения k эффективная масса возрастает, оставаясь положительной. При приближении kк точкам -p/2а и p/2а величинаd²E/dk² положительна и уменьшается до нуля. Поэтому эффективная масса m* стремится к +¥ и в точках -p/2а и p/2а претерпевает разрыв.

В точках -p/а и p/а величина d²E/dk² по абсолютной величине максимальна и отрицательна. Поэтому на краях зоны Бриллюэна, на потолке энергетической зоны в рассматриваемом случае, эффективная масса электрона m* минимальна и отрицательна. По мере уменьшения абсолютного значения k величина m* возрастает по модулю, оставаясь отрицательной. При приближении k к точкам -p/2а и p/2а функция m* = f(k) стремится к -¥, то есть претерпевает разрыв.

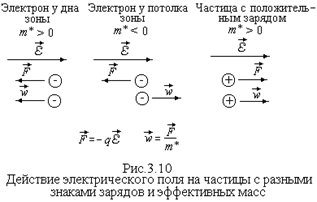Полученный график говорит о том, что у дна энергетической зоны эффективная масса электрона m* минимальна и положительна. Такие электроны, при соответствующих условиях, реагируют на внешнее электрическое поле и ускоряются в направлении противоположном вектору напряженности поля (рис.3.10). По мере увеличения энергии электрона, смещении его к середине разрешенной энергетической зоны, величина m* возрастает и его рeакция на электрическое поле ослабевает. Если электрон находится по середине энергетической зоны, его эффективная масса стремится к бесконечности, такой электрон не будет реагировать на внешнее электрическое поле.

У потолка зоны эффективная масса электрона отрицательна. Поэтому, несмотря на то, что сила, 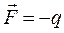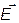, действующая со стороны поля, направ­лена противоположно полю, ускорение электрона происходит в направлении электрического поля.

Но точно также будет реагировать на электрическое поле частица с положительным зарядом и положительной эффективной массой.

Поэтому можно говорить, что электрон у потолка разрешенной энергетической зоны подобен частице с положительным зарядом, численно равным заряду электрона, и положительной массой, численно равной отрицательной эффективной массе электрона.