Математическое моделирование и САПР электронных схем

Под математическим моделированием (мм) имеют в виду создание некоторого абстрактного аналога реального объекта (схемы замещения и математической модели) и получение той или иной информации об атом идеализированном объекте (реализация модели). Разумеется, имеет смысл рассматривать идеализированный объект, если он достаточно адекватен реальному объекту. В то же время судить о степени адекватности заранее не всегда представляется возможным. Обычно это выверяется в процессе практической деятельности, то есть материализации идеального объекта. Поэтому, чем сложнее реальный объект и его модель, тем большую степень риска приходится допускать с точки зрения затрат ресурсов и труда. Многократная реализация модели позволяет получить всю необходимую информацию об объекте, т.е. провести анализ. Обычно под анализом понимают получение информации при фиксированном наборе параметров объ­екта. Поскольку проектируемый объект должен удовлетворять требованиям технического задания, параметры следует подбирать так, чтобы информация об объекте соответствовала определенным условиям. Эти условия формируют в виде целевых функций, а сам процесс подбора параметров называют параметрический оптимизацией.

Возможность автоматизации формирования математических моделей электронных устройств естественно привела к идее автоматизации вес. процесса проектирования, которая нашла свое воплощение в концепции САПР [3;25] , включающей в себя комплекс средств автоматизации проектирования. Процесс проектирования на основе мм, осуществляемый в САПР, в самом общем виде можно представить в виде блок-схемы рис. I. Выбор структуры, наиболее творческая и наиболее трудно формализуемая часть проектирования, обычно осуществляется разработчиком на основе технического задания и анализа готовых структур, накопленных в процессе практической и изобретательской деятельности. После формирования модели, с точки зрения проектирования важной представляется та часть блок-схемы рис. 1, которая связана с оптимизацией. Роль анализа заключается в предварительном исследовании объекта и подборе начальных значений параметров. После оптимизации, естественно, может возникнуть необходимость получения дополнительной информации об объекте, для чего также используется блок анализа.

Реализация математической модели предполагает следующую последовательность действии:

1) выбор цели реализации;

2) выбор метода расчета;

3) выбор численной схемы;

4) составление алгоритма и программы;

5) счёт и обработка результатов.

Выбор цели определяет направленность действий, а её реализация (достижение) доставляет определенную информацию об объекте. Все указанные этапы реализации должны осуществляться в блоке реализации математических моделей автоматически.

В настоящее время уже создано большое количество систем автоматизированного анализа и параметрической оптимизации (см. например, [2б,27,28]). Их развитие прежде всего связано с развитием блока реализации математических моделей. В частности, из-за узости возможностей методов расчета, заложенных в этот, блок, естественно занижаются и возможности указанных систем. В [25] вводится понятие надежности методов и алгоритмов заложенных в САПР. Оценкой надежности является вероятность Р успешного применения метода в оговоренном заранее классе задач. Если говорить о достоинствах САПР с точки зрения их надежности, то в настоящее время она не велика, хотя нет оснований сомневаться в том, что по мере развития методов реализации математических моделей она будет возрастать. Но, по-видимому, создание высоконадежных САПР дело далекого будущего. Именно поэтому нисколько не теряют своего значения традиционные методы формирования и реализации математических моделей, позволяющие более гибко подходить я преодолению трудностей я нестандартных ситуациях.

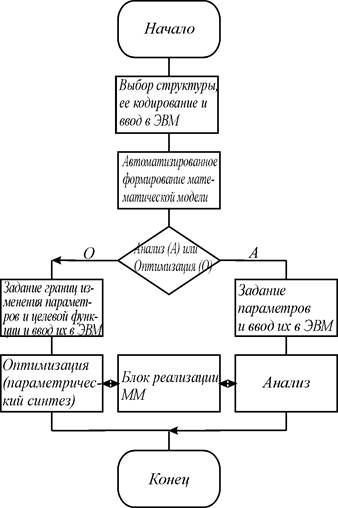
Рис. 1