Фаза 1 сортировки: построение пирамиды
Hачать построение пирамиды можно с a[k]...a[n], k = [(n+1)/2]. Эта часть массива удовлетворяет свойству пирамиды, так как не существует индексов i,j: i = 2i+1 (или j = 2i+2)... Просто потому, что такие i,j находятся за границей массива (на графическом языке – эта часть элементов не имеет потомков).
Далее будем расширять часть массива, обладающую столь полезным свойством, добавляя по одному элементу за шаг. Следующий элемент на каждом шаге добавления - тот, который стоит перед уже готовой частью.
Чтобы при добавлении элемента сохранялась пирамидальность, будем использовать следующую процедуру расширения пирамиды a[i+1]..a[n] на элемент a[i] влево:
1. Смотрим на сыновей слева и справа - в массиве это a[2i+1] и a[2i+2] и выбираем наибольшего из них.
2. Если этот элемент больше a[i] - меняем его с a[i]местами и идем к шагу 2, имея в виду новое положение a[i] в массиве. Иначе конец процедуры.
Новый элемент "просеивается" сквозь пирамиду.
Ниже дана иллюстрация процесса построения для пирамиды из 8-и элементов:
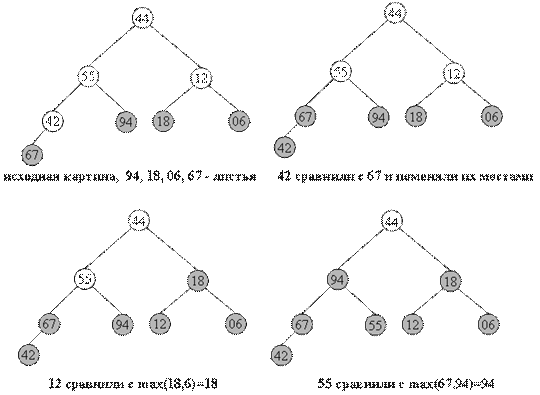
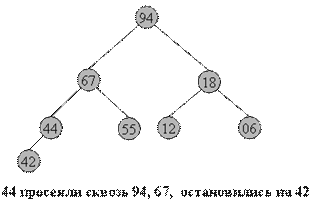
44 55 12 42 // 94 18 06 67 Справа - часть массива, 44 55 12 // 67 94 18 06 42 удовлетворяющая свойству 44 55 // 18 67 94 12 06 42 пирамиды, 44 // 94 18 67 55 12 06 42 остальные элементы добавляются // 94 67 18 44 55 12 06 42один за другим, справа налево
В геометрической интерпретации ключи из начального отрезка a[(n+1)/2]...a[n] являются листьями в бинарном дереве, как изображено ниже. Один за другим остальные элементы продвигаются на свои места, и так - пока не будет построена вся пирамида. На рисунках ниже изображен процесс построения. Неготовая часть пирамиды (начало массива) окрашена в белый цвет, удовлетворяющий свойству пирамиды конец массива - в темный.
Дата добавления: 2022-02-05; просмотров: 434;











