Фаза 2: собственно сортировка

<6 7 8 9 10 1112>

Итак, задача построения пирамиды из массива решена. Как видно из свойств пирамиды, в корне всегда находится максимальный элемент. Отсюда вытекает алгоритм фазы 2:

1. Берем верхний элемент пирамиды a[0]...a[n] (первый в массиве) и меняем с последним местами. Теперь "забываем" об этом элементе и далее рассматриваем массив a[0]...a[n-1]. Для превращения его в пирамиду достаточно просеять лишь новый первый элемент.

2. Повторяем шаг 1, пока обрабатываемая часть массива не уменьшится до одного элемента.

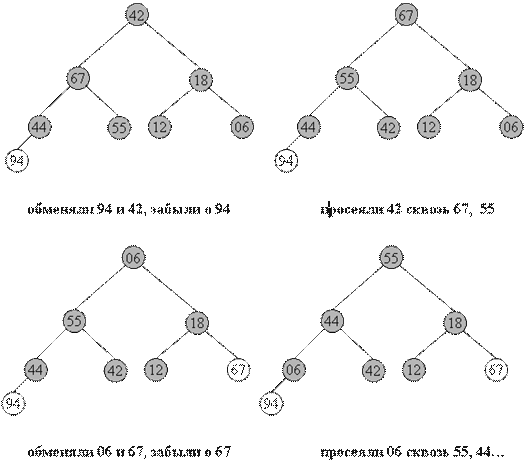
Очевидно, в конец массива каждый раз попадает максимальный элемент из текущей пирамиды, поэтому в правой части постепенно возникает упорядоченная последовательность.

94 67 18 44 55 12 06 42 // иллюстрация 2-й фазы 67 55 44 06 42 18 12 // 94 сортировки пирамиды 55 42 44 06 12 18 // 67 94 44 42 18 06 12 // 55 67 94 42 12 18 06 // 44 55 67 94 18 12 06 // 42 44 55 67 94 12 06 // 18 42 44 55 67 94 06 // 12 18 42 44 55 67 94

Построение пирамиды занимает O(n log n) операций, причем более точная оценка дает даже O(n) за счет того, что реальное время выполнения downheap зависит от высоты уже созданной части пирамиды. Вторая фаза занимает O(n log n) времени: O(n) раз берется максимум и происходит «просеивание» бывшего последнего элемента. Плюсом является стабильность метода: среднее число пересылок (n log n)/2, и отклонения от этого значения сравнительно малы.

Пирамидальная сортировка не использует дополнительной памяти. Метод не является устойчивым: по ходу работы массив так «перетряхивается», что исходный порядок элементов может измениться случайным образом. Поведение неестественно: частичная упорядоченность массива никак не учитывается.

3. Быстрая сортировка

"Быстрая сортировка", хоть и была разработана 50 лет назад, является широко применяемым и одним их самых эффективных алгоритмов. Общая схема такова:

1. из массива выбирается некоторый опорный элемент a[i],

2. запускается процедура разделения массива, которая перемещает все ключи, меньшие, либо равные a[i], влево от него, а все ключи, большие, либо равные a[i] - вправо,

3. теперь массив состоит из двух подмножеств, причем левое меньше, либо равно правого,

4. для обоих подмассивов: если в подмассиве более двух элементов, рекурсивно запускаем для него ту же процедуру.

В конце получится полностью отсортированная последовательность.

Рассмотрим алгоритм подробнее.

Разделение массива

На входе массив a[0]...a[N] и опорный элемент p, по которому будет производиться разделение.

1. Введем два указателя: i и j. В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности.

2. Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p. Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p.

3. Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i,j по тем же правилам.

4. Повторяем шаг 3, пока i <= j.

Рассмотрим работу процедуры для массива a[0], ... , a[6] и опорного элемента p = a[3].

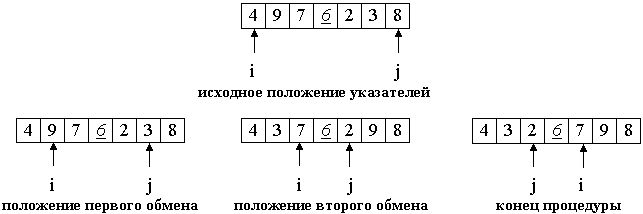
Теперь массив разделен на две части: все элементы левой меньше либо равны p, все элементы правой - больше, либо равны p. Разделение завершено.

Общий алгоритм

quickSort ( массив a, верхняя граница N ) { Выбрать опорный элемент p - середину массива Разделить массив по этому элементу Если подмассив слева от p содержит более одного элемента, вызвать quickSort для него. Если подмассив справа от p содержит более одного элемента, вызвать quickSort для него. }

Реализация на Си для int.

void quickSortR(int* a, long N) {// На входе - массив a[], a[N] - его последний элемент. long i = 0, j = N; // поставить указатели на исходные места int temp, p; p = a[ N>>1 ]; // центральный элемент//---------------------------------- процедура разделения do { while ( a[i] < p ) i++; while ( a[j] > p ) j--; if (i <= j) { temp = a[i]; a[i] = a[j]; a[j] = temp; i++; j--; } } while ( i<=j ); // рекурсивные вызовы, если есть, что сортировать if (j > 0) quickSortR(a, j); if (N > i) quickSortR(a+i, N-i);}

Количество шагов деления (глубина рекурсии) составляет приблизительно log n, если массив делится на более-менее равные части. Таким образом, общее быстродействие: O(n log n), что и имеет место на практике.

Однако, возможен случай таких входных данных, на которых алгоритм будет работать за O(n²) операций. Такое происходит, если каждый раз в качестве центрального элемента выбирается максимум или минимум входной последовательности. Если данные взяты случайно, вероятность этого равна 2/n. И эта вероятность должна реализовываться на каждом шаге. Вообще говоря, малореальная ситуация.

Метод неустойчив. Поведение довольно естественно, если учесть, что при частичной упорядоченности повышаются шансы разделения массива на более равные части.

Сортировка использует дополнительную память, так как приблизительная глубина рекурсии составляет O(log n), а данные о рекурсивных подвызовах каждый раз добавляются в стек.

Замечания:

1. Из-за рекурсии и других "накладных расходов" Quicksort может оказаться не столь уж быстрой для коротких массивов. Поэтому, если в массиве меньше C элементов (константа зависит от реализации, обычно равна от 3 до 40), вызывается сортировка вставками. Увеличение скорости может составлять до 15%.

2. В случае явной рекурсии в стеке сохраняются не только границы подмассивов, но и ряд совершенно ненужных параметров, таких как локальные переменные. Если эмулировать стек программно, его размер можно уменьшить в несколько раз.

3. Чем на более равные части будет делиться массив – тем лучше. Потому в качестве опорного целесообразно брать средний из трех, а если массив достаточно велик – то из девяти произвольных элементов.

4. Пусть входные последовательности очень плохи для алгоритма. Например, их специально подбирают, чтобы средний элемент оказывался каждый раз минимумом. Можно просто выбирать в качестве опорного случайный элемент входного массива. Тогда любые неприятные закономерности во входном потоке будут нейтрализованы. Другой вариант - переставить перед сортировкой элементы массива случайным образом.

5. Быструю сортировку можно использовать и для двусвязных списков. Единственная проблема - отсутствие непосредственного доступа к случайному элементу. Так что в качестве опорного приходится выбирать первый элемент, и либо надеяться на хорошие исходные данные, либо случайным образом переставить элементы перед сортировкой.

6. Можно заменить рекурсию на итерации, реализовав стек на основе массива. Процедура разделения будет выполняться в виде цикла. Каждый раз, когда массив делится на две части, в стек будет направляться запрос на сортировку большей из них, а меньшая будет обрабатываться на следующей итерации. Запросы будут выбираться из стека по мере освобождения процедуры разделения от текущих задач. Сортировка заканчивает свою работу, когда запросы кончаются.

4. Сортировка слиянием

Сортировка слиянием также построена на принципе "разделяй-и-властвуй", однако реализует его несколько по-другому, нежели quickSort. А именно, вместо разделения по опорному элементу массив просто делится пополам.

//a - сортируемый массив, его левая граница lb,правая граница ubvoid mergeSort(int a[], long lb, long ub) { long split; // индекс, по которому делим массив if (lb < ub) { // если есть более 1 элемента split = (lb + ub)/2; mergeSort(a, lb, ub); // сортировать левую половину mergeSort(a, split+1, last);// сортировать правую половину merge(a, lb, split, ub); }}

Функция merge на месте двух упорядоченных массивов a[lb]...a[split] и a[split+1]...a[ub] создает единый упорядоченный массив a[lb]...a[ub].

Пример работы алгоритма на массиве 3 7 8 2 4 6 1 5.. (split – трещина, раскол)

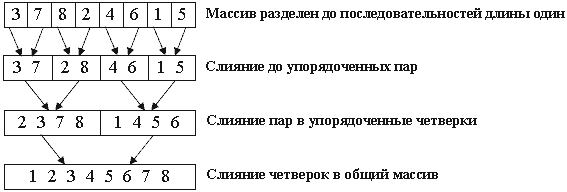
Рекурсивный алгоритм обходит получившееся дерево слияния в прямом порядке. Каждый уровень представляет собой проход сортировки слияния - операцию, полностью переписывающую массив. Обратим внимание, что деление происходит до массива из единственного элемента. Такой массив можно считать упорядоченным, а значит, задача сводится к написанию функции слияния merge (мэдж).

Один из способов состоит в слиянии двух упорядоченных последовательностей при помощи вспомогательного буфера, равного по размеру общему количеству имеющихся в них элементов. Элементы последовательностей будут перемещаться в этот буфер по одному за шаг.

merge ( упорядоченные последовательности A, B , буфер C ) { пока A и B непусты { cравнить первые элементы A и B переместить наименьший в буфер } если в одной из последовательностей еще есть элементы дописать их в конец буфера, сохраняя имеющийся порядок}

Хорошо запрограммированная внутренняя сортировка слиянием работает немного быстрее пирамидальной, но медленнее быстрой, при этом требуя много памяти под буфер. Поэтому mergeSort используют для упорядочения массивов, лишь если требуется устойчивость метода (которой нет ни у быстрой, ни у пирамидальной сортировок). Сортировка слиянием является одним из наиболее эффективных методов для односвязных списков и файлов, когда есть лишь последовательный доступ к элементам.