Многосвязные (слоеные) списки
В одном элементе списка можно указать сколько угодно связей и в этом случае нам придется иметь дело с многосвязными списками, или как их еще называют – «слоеными списками». Так, например, в автоматизированной системе учета лиц, пострадавших вследствие аварии на ЧАЭС, каждая запись об одном пострадавшем содержит более 50 полей в своей информационной части.

Рис. 12: Пример мультисписка
Для того, чтобы при выборке каждого подмножества не выполнять полный просмотр с отсеиванием записей, к требуемому подмножеству не относящихся, в каждую запись включаются дополнительные поля ссылок, каждое из которых связывает в линейный список элементы соответствующего подмножества. В результате получается многосвязный список или мультисписок, каждый элемент которого может входить одновременно в несколько односвязных списков. Пример такого мультисписка для названной нами автоматизированной системы показан на рис.12.
Каждая подзадача работает со своим подмножеством как с линейным списком, используя для этого определенное поле связок. Специфика мультисписка проявляется только в операции исключения элемента из списка. Исключение элемента из какого-либо одного списка еще не означает необходимости удаления элемента из памяти, так как элемент может оставаться в составе других списков. Память должна освобождаться только в том случае, когда элемент уже не входит ни в один из частных списков мультисписка. Обычно задача удаления упрощается тем, что один из частных списков является главным - в него обязательно входят все имеющиеся элементы. Тогда исключение элемента из любого неглавного списка состоит только в переопределении указателей, но не в освобождении памяти. Исключение же из главного списка требует не только освобождения памяти, но и переопределения указателей как в главном списке, так и во всех неглавных списках, в которые удаляемый элемент входил.
Алгоритмы поиска.
1. Поиск
Поиск – это одно из наиболее часто встречающихся в программировании действий. Существует множество разнообразных алгоритмов поиска, связанных как со способом представления информации, ее организацией, так и методов его проведения. Однако принципиальным является следующее допущение: группа данных, в которой необходимо отыскать заданный элемент, фиксирована. Т.е. предполагается, что существует некоторый массив а[] элементов. Вне зависимости от конкретного типа элементов этого массива предполагается наличие ключа поиска, т.е. такого поля, для которого можно осуществлять проверку на совпадение с некоторым искомым образцом х. Поскольку вся прочая информация из элемента массива нас не интересует, то можно считать, что поиск проводится в массиве, элементы которого и есть ключи поиска.
Если нет никакой дополнительной информации о разыскиваемых данных, то очевидный подход – простой последовательный просмотр элементов массива. Такой подход называется линейным поиском. Условия окончания поиска таковы:
Элемент найден, т.е. а[i] = х.
Весь массив просмотрен и совпадения не обнаружено.
Алгоритм:
i=0;
while(( i < N) && (a[i]!=x)) i++;
По завершению цикла равенство (i==N) свидетельствует, что искомого элемента в массиве не существует.
Можно ли ускорить представленный алгоритм? Единственная возможность – упростить проверяемое условие, заменив его на более простое эквивалентное. Для этого достаточно в конец массива поместить дополнительный элемент со значением х. Назовем такой вспомогательный элемент «барьером», поскольку он предохраняет нас от перехода за пределы массива.
Алгоритм:
A[N] = x; i=0;
while(a[i++]!=x);
В итоге, как и ранее, равенство (i==N) свидетельствует, что искомого элемента в массиве не существует.
2. Бинарный поиск
Далее без дополнительной информации об организации массива улучшить данный алгоритм поиска не представляется возможным. Но поиск можно сделать гораздо более эффективным, если данные в массиве будут упорядочены. Это значит, что выполняется условие
A[k-1] <= A[k] для k=1,2,…,N
Основная идея алгоритма – выбрать случайно некоторый элемент, предположим am, и сравнить его с искомым х. Если он равен х, то поиск заканчивается; если он меньше х, то можно сказать, что все элементы с индексами не большими m из дальнейшего поиска можно исключить; если же х > am, то из рассмотрения исключаются индексы, большие или равные m. В итоге имеем алгоритм, называемый «поиском деления пополам». Здесь две индексные переменные L и R отмечают соответственно левый и правый конец секции массива a, где еще может быть обнаружен требуемый элемент.
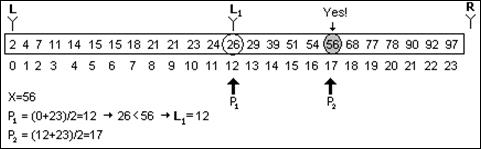
int FindD2 (int* A, int N, int X )
{
int m, L=0, R=N-1, flag=0;
while (L<=R && !flag)
{
m=(L+R)/2;
if (A[m]==X) flag = 1;
else if (A[m]<X) L=m+1;
else R=m-1;
}
return flag;
}
Выбор в качестве значения m не случаен. Именно в этом случае обеспечивается исключение из рассмотрения наибольшего количества элементов массива. В результате максимальное число сравнений равно log N, округленному до ближайшего целого. Таким образом, приведенный алгоритм существенно выигрывает по сравнению с алгоритмом линейного поиска, для которого число сравнений равно N/2.
3. Алгоритм прямого поиска строки
Часто приходится сталкиваться со специфическим поиском, так называемым поиском строки. Эту задачу можно определить так.
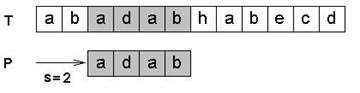
Пусть задан массив s из N элементов и массив p из M элементов, причем 0<M<=N. Поиск строки обнаруживает первое вхождение p в s. Можно считать, что s – это некоторый текст, а p - некоторое слово и требуется найти первое вхождение этого слова в указанный текст. Это действие является типичным для любых систем обработки текстов и в силу этого крайне важно использование высокоэффективных алгоритмов.
Но сначала разберем простейший алгоритм, называемый прямым поиском строки.
Результатом поиска будем считать индекс i, указывающий на первое от начала строки совпадение с образцом. С этой целью введем предикат P(i,j):
P(i,j) = Ak: 0 <= k < j: si+k = pk
Результирующий индекс, очевидно должен удовлетворять этому предикату P(i,M). Но этого недостаточно – ведь поиск должен обнаруживать первое вхождение образца, и значит P(k,M) должно быть ложным для всех k<i:
Q(i) = Ak: 0 <= k < i: ~P(k,M)
Условно алгоритм можно описать следующим образом
i=-1;
do
{
i++; j=0; // Q(i)
while ((j<M) && (s[i+j] == p[j]) ) j++;
// Q(i) && P(i,j) && ((j==M) || (s[i+j] != p[j]))
} while (j<M && i < N-M);
Этот алгоритм работает достаточно эффективно, если допустить, что несовпадение пары символов происходит после всего нескольких операций сравнений во внутреннем цикле. Если же взять в качестве текста АААААААВ и искать в нем AAВ – то в общем случае может понадобиться N*M операций.
4. Алгоритм Кнута-Мориса-Пратта
Приблизительно в 1970 году ученые Кнут, Морис и Пратт изобрели алгоритм, фактически требующий только N сравнений даже в самом плохом случае.
Идея алгоритма в том, что, начиная каждый раз сравнение образца с самого начала, можем уничтожать полезную информацию. После частичного совпадения начальной части образца с соответствующими символами текста фактически известна пройденная часть текста и можно «вычислить» некоторые сведения (на основе самого образца), с помощью которых потом быстро продвинемся по тексту. Рассмотрим пример.
Hoola–Hoola girls like Hooligans.
Hooligan
Hooligan
Hooligan
Hooligan
Hooligan
. . .
Используя предикаты P и Q, KMP-алгоритм можно условно записать так:
i=0; j=0;
while(j<M && i<N)
{
while(j>=0 && s[i]!=p[j]) j=D;
i++; j++;
}
Итак, дадим несколько определений:
Текст: строка s[N].
Искомый образец: p[M].
Алфавит - множество символов, из которых составлены текст и образец - a[A].
Слово u - префикс слова w, если существует слово v: w=uv.
Слово v - суффикс слова w, если существует слово u: w=uv.
Слово z - граница слова w, если существуют u и w: w=uz=zv, т.е. z - одновременно префикс и суффикс w.
Для произвольного слова X рассмотрим все его границы, и выберем среди них самую длинную (не считая самого X). Обозначим ее L(X). Например, L(abcab)=ab, L(cabcabc)=cabc. Функцию F(X), задающую длину максимальной границы слова X, будем называть префикс-функцией. Например, F(abcab)=2, F(cabcabc)=4.
Для вычисления сдвига D, нам понадобится вычислить значения F() для всех границ искомого образца.
Далее F[k] будет означать F(p[1..K]). Если рассмотреть последовательность слов X, L(X), L(L(X)), L(L(L(X))), … то легко видеть, что каждый следующий ее элемент будет префикс-суффиксом предыдущего, и эта последовательность оканчивается пустой строкой. Последовательность чисел
length(X), F(X), F(F(X)), F(F(F(X)))… (соответствующая вышеупомянутой) убывает и оканчивается нулем. Алгоритм вычисления F[k] будет следующим. Допустим, мы уже вычислили F[1], ..., F[k-1]. На k-м шаге нам надо вычислить F[k].
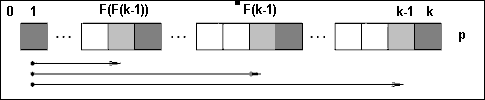
Рассмотрим p[k]. Символы, которые будем сравнивать, обозначены темно-серым цветом.
Если p[k] = p[F[k-1]+1] , то F[k] = F[k-1] + 1 (так как p[1..F[k-1]] – суффикс p[1..k-1], и, следовательно, p[1..F[k-1]+1] – суффикс p[1..k]).
Если же p[k] <> p[F(k-1)+1], то сравним p[k] с p[F[F[k-1]]+1]. Если последние равны, то F[k] = F[F[k-1]]+1. И так далее. Таким образом, придем к F[k] = F (q)[k-1]+1 (индекс q означает номер итерации) или к F[k]=0, если не существует префикс-суффикса для слова p[1..k].
Следующая функция делает это:
void CompF(char* pat, int*d)
{
int i, len;
i=0; d[0]=-1;
for(i=1; pat[i]!=0; i++)
{
len = d[i-1];
while (len>-1 && pat[len+1]!=pat[i])
len = d[len];
if (pat[len+1] == pat[i]) d[i]=len+1; else d[i]=-1;
}
}
Например, для образца ABDABD в массиве d окажутся значения: -1,-1,-1,0,1,2.
Это значит, что при несовпадении на i-ой позиции образец можно подвинуть по тексту на:
0: 0 - (-1) = 1 1: 1 – (-1) = 2 2: 2 – (-1) = 3
3: 3 – 0 = 3 4: 4 – 1 = 3 5: 5 – 2 = 3
Воспользовавшись представленной функцией, программу, осуществляющую поиск по KMP-алгоритму, можно записать так:
int FindKMP (char* text,char* pat )
{
int i, j, lenT, lenP, d[100];
lenT = strlen(text); lenP = strlen(pat);
CompF(pat, d);
i=0; j=-1;
for (i=0; i < lenT; i++)
{
while (j>=0 && text[i]!=pat[j+1]) j = d[j];
if (text[i] == pat[j+1]) j++;
if (j+1==lenP) return 1;
}
return 0;
}
Анализ КМП-алгоритма. Сложность подготовительного этапа алгоритма – O(m). Этот вывод можно сделать из следующего соображения:
F[i] <= F[i-1] – (число операций на i-м шаге) + 1
(так как каждая итерация while уменьшает len как минимум на 1). Сложив все такие неравенства по i=2,...,m, получим, что общее число операций не больше сm, где с – некая константа. Таким образом, учетная стоимость i-й итерации for не превосходит О(1).
Применив аналогичные рассуждения к основному этапу, получим, что общая сложность алгоритма равна O(m+n), что намного меньше, чем O(m(n-m+1)), как в случае самого простого алгоритма. Количество памяти, необходимое для алгоритма – O(m) (для запоминания префикс-функции).
5. Алгоритм Боуера-Мура
Рассмотренный нами алгоритм КМП дает существенный выигрыш только тогда, когда неудаче предшествует некоторое количество совпадений. Только в этом случае образ сдвигается более чем на 1. К сожалению, для реальных текстов это скорее исключение, чем правило.
Сейчас рассмотрим еще один алгоритм, который не только улучшает обработку самого плохого случая, но и дает выигрыш в промежуточных ситуациях. Его предложили Боуер и Мур примерно в 1975 году.
БМ-поиск основывается на необычном соображении – сравнение символов начинается с конца образа, а не с начала. Как и в случае КМП-алгоритма, образ сначала трансформируется в некоторую таблицу.
Пусть для каждого символа х из алфавита dх – расстояние от самого правого в образе вхождения х до его конца (правого). Пусть возникло расхождение между образом и строкой. В этом случае образ сразу же можно сдвинуть вправо на dpM-1 позиций, т.е. на число позиций, скорее всего больше 1. Если символ, соответствующий конечному символу образа вообще не встречается в образе, то можно сдвигаться на величину всего образа.
Рассмотрим пример.
Hoola–Hoola girls like Hooligans.
 Hooligan
Hooligan
Hooligan
Hooligan
Hooligan
Hooligan
Программа, реализующая БМ-алгоритм может быть представлена так:
#include <string.h>
#include <stdio.h>
#define ASIZE 256
int BM(char* text, char *pattern, int n, int m)
{
int i;
int d[ASIZE];
//preprocessing...
for (i=0;i<ASIZE;i++) d[i] = m + 1;
for (i=0;i<m;i++) d[pattern[i]] = m - i;
//actual search...
i = 0;
while (i <= n - m)
{
printf("%s\n",&text[i]);
if (memcmp(&text[i],pattern,m) == 0) return i+1;
i = i + d[text[i + m]];
}
return 0;
}
void main()
{
char text[100], pattern[100];
printf("\nInput text:\n");
gets(text);
do
{
fflush(stdin);
strcpy(pattern,"");
printf("\nInput pattern:\n");
gets(pattern);
if (pattern[0] == '.') break;
if (pattern[0] == '?') { printf("\n%s",text); continue; }
if (BM( text, pattern, strlen(text), strlen(pattern) ))
printf("\n TRUE\n");
else
printf("\n FALSE");
} while (1);
}
6. Сравнительный анализ известных алгоритмов
| Алгоритм | Время на предварит. обработку | Среднее время поиска | Худшее время поиска | Примечания |
| Алгоритм прямого сравнения | Нет | 2*n | O(n*m) | Mалые трудозатраты на программу |
| Алгоритм KMP | O(m) | O(n+m) | O(n+m) | - |
| Алгоритм БМ | O(m+s) | O(n+m) | O(n*m) | Алгоритмы этой группы наиболее эффективны в обычных ситуациях. Быстродействие повышает-ся при увеличении образца или алфавита. |
7. Многократный поиск на основе использования статистических данных.
Предположим теперь, что нам предлагается осуществлять поиск заданного образца в каком-то большом, но неизменяемом тексте. В этом случае большим подспорьем может стать информация о частоте вхождений в текст символов из алфавита. Для заданного образца определяется наименее используемый в строке символ и далее алгоритм основан на перемещении по образцу с помощью перехода на следующий «редкий символ». Алгоритм может сочетать в себе элементы ранее рассмотренных алгоритмов.
Алгоритмы сортировки.
1. Сортировки – общая классификация
Пусть есть последовательность a0, a1... an и функция сравнения, которая на любых двух элементах последовательности принимает одно из трех значений: меньше, больше или равно. Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие: ai <= ai+1, для всех i от 0 до n.
Естественно, что возможна ситуация, когда элементы состоят из нескольких полей:
 struct element { int x; int y; }
struct element { int x; int y; } Если значение функции сравнения зависит только от поля x, то x называют ключом, по которому производится сортировка. На практике, в качестве x часто выступает число, а поле y хранит какие-либо данные, никак не влияющие на работу алгоритма.
Пожалуй, никакая другая проблема не породила такого количества разнообразнейших решений, как задача сортировки. Существует ли некий "универсальный", наилучший алгоритм? Вообще говоря, нет. Однако, имея приблизительные характеристики входных данных, можно подобрать метод, работающий оптимальным образом.
Для того, чтобы обоснованно сделать такой выбор, рассмотрим параметры, по которым будет производиться оценка алгоритмов.
1. Время сортировки - основной параметр, характеризующий быстродействие алгоритма.
2. Память - ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы.
3. Устойчивость - устойчивая сортировка не меняет взаимного расположения равных элементов. Такое свойство может быть очень полезным, если они состоят из нескольких полей, как на рис. 1, а сортировка происходит по одному из них, например, по x.
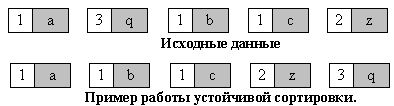
Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" осталось прежним: элемент с полем "a", затем - с "b", затем - с "c".

Взаимное расположение равных элементов с ключом 1 и дополнительными полями "a", "b", "c" изменилось.
4. Естественность поведения - эффективность метода при обработке уже отсортированных, или частично отсортированных данных. Алгоритм ведет себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.
Еще одним важным свойством алгоритма является его сфера применения. Здесь основных позиций две:
внутренние сортировки работают с данным в оперативной памяти с произвольным доступом;
внешние сортировки упорядочивают информацию, расположенную на внешних носителях. Это накладывает некоторые дополнительные ограничения на алгоритм:
- доступ к носителю осуществляется последовательным образом: в каждый момент времени можно считать или записать только элемент, следующий за текущим
- объем данных не позволяет им разместиться в ОЗУ
Кроме того, доступ к данным на носителе производится намного медленнее, чем операции с оперативной памятью.
Данный класс алгоритмов делится на два основных подкласса:
Внутренняя сортировка оперирует с массивами, целиком помещающимися в оперативной памяти с произвольным доступом к любой ячейке. Данные обычно сортируются на том же месте, без дополнительных затрат.
Внешняя сортировка оперирует с запоминающими устройствами большого объема, но с доступом не произвольным, а последовательным (сортировка файлов), т.е. в данный момент «видим» только один элемент, а затраты на перемотку по сравнению с памятью неоправданно велики. Это приводит к специальным методам сортировки, обычно использующим дополнительное дисковое пространство.
Займемся сначала прямыми методами сортировок, в которых требуется порядка n2 сравнений ключей. А почему не более быстрыми? На то есть три причины:
· Прямые методы особенно удобны для объяснения характерных черт основных принципов большинства сортировок.
· Программы прямых методов легко понимать, и они коротки.
· Усложненные методы требуют небольшого числа операций, но эти операции обычно сами более сложны, и поэтому для достаточно малых n прямые методы оказываются быстрее, хотя для больших n их использовать не следует.
2. Сортировка с помощью вставки (включения)
Этот метод сортировки широко используется при игре в карты. Элементы (карты) мысленно делятся на уже готовую последовательность a[0]...a[i] и исходную. При каждом шаге, начиная с первого, i увеличивается каждый раз на единицу, из исходной последовательности извлекается i-ый элемент и перекладывается в готовую последовательность, при этом он вставляется на нужное место.
Пример.
i = 0 44 55 12 42 94 18 06 67
i = 1 44 55 12 42 94 18 06 67
i = 2 12 44 55 42 94 18 06 67
i = 3 12 42 44 55 94 18 06 67
i = 4 12 42 44 55 94 18 06 67
i = 5 12 18 42 44 55 94 06 67
i = 6 06 12 18 42 44 55 94 67
i = 7 06 12 18 42 44 55 67 94
Будем разбирать алгоритм, рассматривая его действия на i-м шаге. Как говорилось выше, последовательность к этому моменту разделена на две части: готовую a[0]...a[i] и неупорядоченную a[i+1]...a[n-1]. На следующем, (i+1)-м шаге алгоритма берем a[i+1] и вставляем на нужное место в готовую часть массива.
Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним. В зависимости от результата сравнения элемент либо остается на текущем месте (вставка завершена), либо они меняются местами и процесс повторяется.
Последовательность на текущий момент. Часть a[0], …, a[4] уже отсортирована.
i = 3 12 42 44 55 94 18 06 67
Вставка число 18 в отсортированную последовательность. Пара для сравнения выделена.
i = 0 12 42 44 55 94 18 06 67
j = 1 12 42 44 55 18 94 06 67
j = 2 12 42 44 18 55 94 06 67
j = 3 12 42 18 4455 94 06 67
j = 4 12 18 424455 94 06 67
Таким образом, в процессе вставки "просеиваем" элемент x к началу массива, останавливаясь в случае, когда
1. найден элемент, меньший xили
2. достигнуто начало последовательности.
void insertSort(int* a, long size) { int x; long i, j; for ( i= 1; i < size; i++) //цикл проходов, i - номер прохода { x = a[i];// поиск места элемента в готовой последовательности for ( j=i-1; j>=0 && a[j] > x; j--) a[j+1] = a[j]; a[j+1] = x; }}
Хорошим показателем такой сортировки является весьма естественное поведение: почти отсортированный массив будет досортирован очень быстро. Это, вместе с устойчивостью алгоритма, делает метод хорошим выбором в соответствующих ситуациях.
Алгоритм можно слегка улучшить. Заметим, что на каждом шаге внутреннего цикла проверяются 2 условия. Можно объединить их в одно, поставив в начало массива специальный барьер. Он должен быть заведомо меньше всех остальных элементов массива.
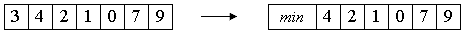
Тогда при j=0 будет заведомо верно a[0] <= x. Цикл остановится на нулевом элементе, что и было целью условия j>=0.
Таким образом, сортировка будет происходить правильным образом, а во внутреннем цикле станет на одно сравнение меньше. С учетом того, что оно производилось О(n2) раз, это - реальное преимущество. Однако, отсортированный массив будет не полон, так как из него исчезло первое число. Для окончания сортировки это число следует вернуть назад, а затем вставить в отсортированную последовательность a[1]...a[n].
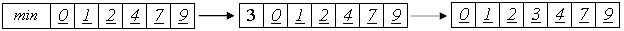
3. Сортировка с помощью выделения (прямого выбора)
Этот алгоритм основан на следующих принципах:
1. Выбирается элемент с наименьшим ключом.
2. Он меняется местами с первым элементом a1.
3. Затем процесс повторяется с оставшимися n-1 элементами, n-2 элементами и т.д. до тех пор, пока не останется один, самый большой элемент.
Посмотрим на примере:
i = 0 44 55 12 42 94 18 06 67
1 06 55 12 42 94 18 44 67
2 06 12 55 42 94 18 44 67
3 06 12 18 42 94 55 44 67
4 06 12 18 42 94 55 44 67
5 06 12 18 42 44 55 94 67
6 06 12 18 42 44 55 94 67
7 06 12 18 42 44 55 67 94
/////////////////// Сортировка выделением ///////////////////void selectSort(int* a, long size) {int x, minE, minP;long i, j; for ( i=0; i < size; i++) // цикл проходов, i - номер прохода { x = a[i]; minE = 0x7fffffff;// поиск в остатке минимального элемента и его места for(j=i; j<size; j++) if(a[j] < minE) { minE = a[j]; minP = j; } a[i] = minE; a[minP] = x; }}4. Сортировка с помощью обменов (пузырьковая сортировка)
Идея метода: шаг сортировки состоит в проходе снизу вверх по массиву. По пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами.
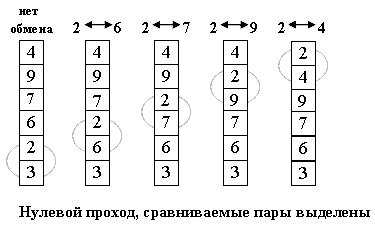
После нулевого прохода по массиву "вверху" оказывается самый "легкий" элемент - отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента, таким образом, второй по величине элемент поднимается на правильную позицию. Делаем проходы по все уменьшающейся нижней части массива до тех пор, пока в ней не останется только один элемент. На этом сортировка заканчивается.
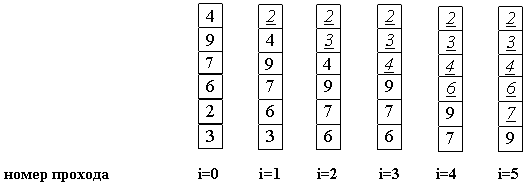
5. Шейкерная сортировка
Алгоритм пузырьковой сортировки можно улучшить, если заметить некоторые особенности его поведения для конкретных примеров. Так, для примера
44 06 06 06 06 06 06 06
55 44 12 12 12 12 12 12
12 55 44 18 18 18 18 18
42 12 55 44 42 42 42 42
94 42 18 55 44 44 44 44
18 94 42 42 55 55 55 55
06 18 94 67 67 67 67 67
67 67 67 94 94 94 94 94
три последних прохода работают вхолостую – все элементы уже отсортированы. Очевидный прием улучшения этого алгоритма – запоминать, были ли перестановки в процессе некоторого прохода, и если нет – заканчивать работу алгоритма. Это улучшение можно опять же улучшить, если запоминать не только сам факт обмена, но и положение (индекс) последнего обмена. Ясно, что все пары соседних элементов выше этого индекса k уже находятся в желаемом порядке. Поэтому просмотры можно заканчивать на этом индексе, а не идти до заранее определенного нижнего предела для i.
Анализируя данный алгоритм можно заметить некоторую асимметрию: всплывает пузы-рек сразу, за один проход, а тонет очень медленно - за один проход на одну позицию:
12 18 42 44 55 67 94 06
94 06 12 18 42 44 55 67
Отсюда и возникает идея третьего улучшения алгоритма: чередовать направление последовательных просмотров. Получающийся при этом алгоритм называется «шейкерной» сортировкой (ShakerSort).
6. Сортировка Шелла
Все строгие приемы сортировки на своем элементарном шаге передвигают каждый элемент на одну позицию. Вследствие этого они требуют порядка n2 таких шагов. В основу любых улучшений должен быть положен принцип перемещения на каждом такте элементов на большие расстояния.
В 1959 году Шеллом было предложено усовершенствование сортировки с помощью прямого включения. Эта сортировка с помощью включений с уменьшающимися расстояниями получила имя автора – сортировка Шелла. Для нашего примера:
Сначала отдельно группируются и сортируются элементы, отстоящие друг от друга на расстоянии 4. В нашем примере 8 элементов и каждая группа состоит точно из двух элементов. После первого прохода элементы перегруппировываются – теперь каждый элемент группы отстоит от другого на две позиции. И наконец на 3-ем проходе идет обычная или ординарная сортировка.
44 55 12 42 94 18 06 67
44 18 06 42 94 55 12 67
06 18 12 42 44 55 94 67
06 12 18 42 44 55 67 94
Получается, что каждая i-сортировка объединяет две группы, уже отсортированные 2i-сортировкой. Видно, что расстояния в группах можно уменьшать по-разному, лишь бы последнее было единичным, ведь в самом плохом случае последний проход и сделает всю работу. Для осознания материала рассмотрим еще один пример
Задан массив a[0].. a[15].
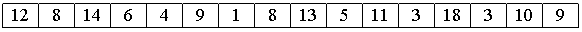
1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).

2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).
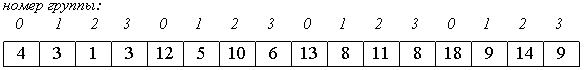
В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.
3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).

4. В конце сортируем вставками все 16 элементов.
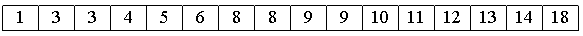
Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам.
Единственной характеристикой сортировки Шелла является приращение (инкремент) - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности. Использованный в примере набор ..., 8, 4, 2, 1 - неплохой выбор, особенно, когда количество элементов - степень двойки. Однако, гораздо лучший вариант предложил Р.Седжвик. Его последовательность имеет вид
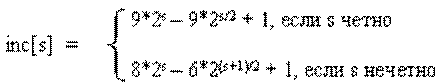
При использовании таких приращений среднее количество операций: O(n7/6), в худшем случае - порядка O(n4/3).
Обратим внимание на то, что последовательность вычисляется в порядке, противоположном используемому: inc[0] = 1, inc[1] = 5, ... Формула дает сначала меньшие числа, затем все большие и большие, в то время как расстояние между сортируемыми элементами, наоборот, должно уменьшаться. Поэтому массив приращений inc вычисляется перед запуском собственно сортировки до максимального расстояния между элементами, которое будет первым шагом в сортировке Шелла. Потом его значения используются в обратном порядке.
При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size.
Часто вместо вычисления последовательности во время каждого запуска процедуры, ее значения рассчитывают заранее и записывают в таблицу, которой пользуются, выбирая начальное приращение по тому же правилу: начинаем с inc[s-1], если 3*inc[s]>size.
int increment(long* inc, long size) { int p1, p2, p3, s; p1 = p2 = p3 = 1; s = -1; do { if (++s % 2) { inc[s] = 8*p1 - 6*p2 + 1; } else { inc[s] = 9*p1 - 9*p3 + 1; p2 *= 2; p3 *= 2; } p1 *= 2; } while(3*inc[s] < size); return s > 0 ? --s : 0;} void shellSort(long* a, long size) { long inc, i, j, seq[40]; int s; // вычисление последовательности приращений s = increment(seq, size); while (s >= 0) { // сортировка вставками с инкрементами inc[] inc = seq[s--]; for (i = inc; i < size; i++) { long temp = a[i]; for (j = i-inc; (j >= 0) && (a[j] > temp); j -= inc) a[j+inc] = a[j]; a[j+inc] = temp; } }}7. Сравнение рассмотренных сортировок
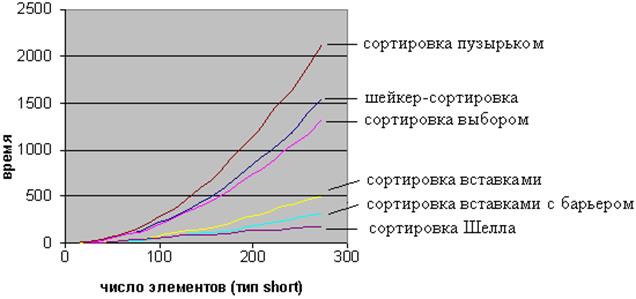
Мы рассмотрели алгоритмы сортировки, имеющие либо квадратичный, либо субквадратич-ный порядок сложности. Изображенный ниже график иллюстрирует разницу в эффективности изученных алгоритмов.
Пирамидальная сортировка
Пирамидальная сортировка является первым из рассматриваемых методов, быстродействие которых оценивается как O(n log n).
В качестве некоторой прелюдии к основному методу, рассмотрим перевернутую сортировку прямым выбором. Во время прохода, вместо вставки наименьшего элемента в левый конец массива, будем выбирать наибольший элемент, а готовую последовательность строить в правом конце.
Пример действий для массива a[0]... a[7]:
44 55 12 42 94 18 06 67 исходный массив 44 55 12 42 67 18 06 |94 94 <-> 67 44 55 12 42 06 18 |67 94 67 <-> 06 44 18 12 42 06 |55 67 94 55 <-> 18 06 18 12 42 |44 55 67 94 44 <-> 06 06 18 12 |42 44 55 67 94 42 <-> 42 06 12 |18 42 44 55 67 94 18 <-> 12 06 |12 18 42 44 55 67 94 12 <-> 12Вертикальной чертой отмечена левая граница уже отсортированной (правой) части массива.
Рассмотрим оценку количества операций подробнее.
Всего выполняется n шагов, каждый из которых состоит в выборе наибольшего элемента из последовательности a[0]… a[i] и последующем обмене. Выбор происходит последовательным перебором элементов последовательности, поэтому необходимое на него время: O(n). Итак, n шагов по O(n) каждый - это O(n 2).
Произведем усовершенствование: построим структуру данных, позволяющую выбирать максимальный элемент последовательности не за O(n), а за O(log n) времени. Тогда общее быстродействие сортировки будет n*O(log n) = O(n log n).
Эта структура также должна позволять быстро вставлять новые элементы (чтобы быстро ее построить из исходного массива) и удалять максимальный элемент (он будет помещаться в уже отсортированную часть массива - его правый конец).
Одной из часто встречающихся при программировании моделей данных является модель дерева. Ее можно определить рекурсивно следующим образом.
Дерево с базовым типом Т – это либо:
1) пустое дерево;
2) некоторая вершина типа Т с конечным числом связанных с ней отдельных деревьев с базовым типом Т, называемых поддеревьями.
Упорядоченное дерево – это дерево, у которого ребра (ветви, дуги), исходящие из каждой вершины упорядочены. На рис. – разные упорядоченные деревья.
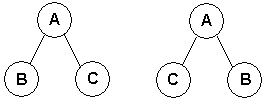
Вершина y, находящаяся непосредственно ниже вершины x, называется непосредственным потомком x; и, наоборот, вершину x называют непосредственным предком y. Употребляют также термины «родитель» и «сын». Все элементы дерева также называют «узлами».
Считается, что корень дерева находится на уровне 0. Максимальный уровень какой-либо из вершин дерева называется его высотой.
Итак, назовем пирамидой (Heap) бинарное дерево высоты k, в котором
- все узлы имеют глубину k или k-1 - дерево сбалансированное.
- при этом уровень k-1 полностью заполнен, а уровень k заполнен слева направо, т.е форма пирамиды имеет приблизительно такой вид:
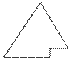
- выполняется "свойство пирамиды": каждый элемент меньше, либо равен родителю.
Как хранить пирамиду? Наименее хлопотно - поместить ее в массив.
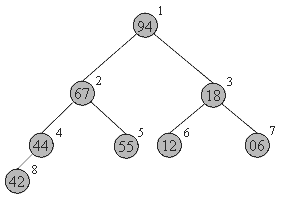
Соответствие между геометрической структурой пирамиды как дерева и массивом устанавливается по следующей схеме:
· в a[0] хранится корень дерева
· левый и правый сыновья элемента a[i] хранятся, соответственно, в a[2i+1] и a[2i+2]
Таким образом, для массива, хранящего в себе пирамиду, выполняется следующее характеристическое свойство: a[i] >= a[2i+1] и a[i] >= a[2i+2].
Плюсы такого хранения пирамиды очевидны:
· никаких дополнительных переменных, нужно лишь понимать схему.
· узлы хранятся от вершины и далее вниз, уровень за уровнем.
· узлы одного уровня хранятся в массиве слева направо.
Запишем в виде массива пирамиду, изображенную выше. Слева-направо, сверху-вниз: 94 67 18 44 55 12 06 42. На рисунке место элемента пирамиды в массиве обозначено цифрой справа-вверху от него.
Восстановить пирамиду из массива как геометрический объект легко - достаточно вспомнить схему хранения и нарисовать, начиная от корня.
Дата добавления: 2022-02-05; просмотров: 762;











