ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
1.1.Уравнение связки плоскостей, проходящих через данную точку 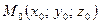 :
:
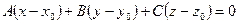 ,
,
где 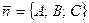 — нормальный вектор плоскости.
— нормальный вектор плоскости.
1.2.Общее уравнение плоскости:
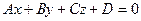 ,
,
где 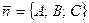 — нормальный вектор плоскости.
— нормальный вектор плоскости.
1.3.Уравнение плоскости, проходящей через три данные точки:
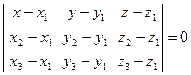 ,
,
где 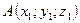 ,
, 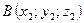 ,
, 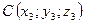 — точки, лежащие на плоскости.
— точки, лежащие на плоскости.
1.4.Угол между плоскостями:
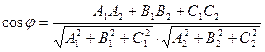 ,
,
где 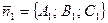 — нормальный вектор первой плоскости,
— нормальный вектор первой плоскости, 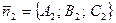 —нормальный вектор второй плоскости.
—нормальный вектор второй плоскости.
1.5.Условие параллельности двух плоскостей:
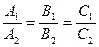 ,
,
где 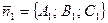 — нормальный вектор первой плоскости,
— нормальный вектор первой плоскости, 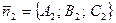 —нормальный вектор второй плоскости.
—нормальный вектор второй плоскости.
1.6.Условие перпендикулярности плоскостей:
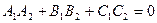 ,
,
где 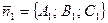 — нормальный вектор первой плоскости,
— нормальный вектор первой плоскости, 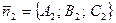 —нормальный вектор второй плоскости.
—нормальный вектор второй плоскости.
1.7.Расстояние от точки до плоскости:
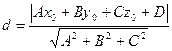 ,
,
где 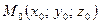 — точка,
— точка, 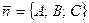 — нормальный вектор плоскости.
— нормальный вектор плоскости.
2. ПРЯМАЯ В ПРОСТРАНСТВЕ
2.1.Канонические уравнения прямой:
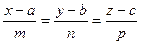 ,
,
где 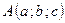 — координаты точки на прямой,
— координаты точки на прямой, 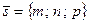 — направляющий вектор прямой.
— направляющий вектор прямой.
2.2.Общие уравнения прямой (прямая задана пересечением двух плоскостей):
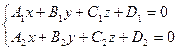 .
.
2.3.Параметрические уравнения прямой:
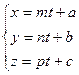 ,
,
где 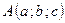 — координаты точки на прямой,
— координаты точки на прямой, 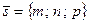 — направляющий вектор прямой,
— направляющий вектор прямой, 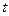 — параметр или вспомогательная переменная.
— параметр или вспомогательная переменная.
2.4.Уравнения прямой, проходящей через две точки:
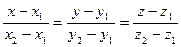 ,
,
где 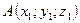 ,
, 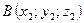 — точки, принадлежащие прямой.
— точки, принадлежащие прямой.
2.5.Угол между двумя прямыми:
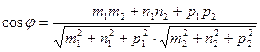 ,
,
где 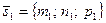 — направляющий вектор первой прямой,
— направляющий вектор первой прямой, 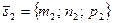 — направляющий вектор второй прямой.
— направляющий вектор второй прямой.
2.6.Условие параллельности двух прямых:
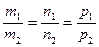 .
.
2.7.Условие перпендикулярности двух прямых:
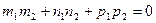 .
.
3. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
3.1.Угол между прямой и плоскостью:
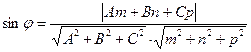 ,
,
где 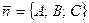 — нормальный вектор плоскости,
— нормальный вектор плоскости, 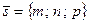 — направляющий вектор прямой.
— направляющий вектор прямой.
3.2.Условие параллельности прямой и плоскости:
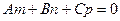 .
.
3.3.Условие перпендикулярности прямой и плоскости:
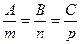 .
.
3.4.Уравнение пучка плоскостей, проходящих через данную прямую:
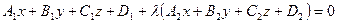 ,
,
где 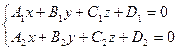 — общие уравнения прямой.
— общие уравнения прямой.
3.5.Условие принадлежности прямой плоскости:
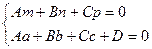 .
.
3.6.Условие того, что две прямые лежат в одной плоскости:
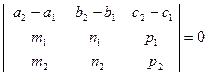 .
.
4. ДРУГИЕ ФОРМУЛЫ
4.1.Координаты середины отрезка
Пусть точка 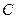 — середина отрезка
— середина отрезка 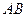 , где
, где 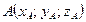 ,
, 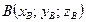 тогда её координаты:
тогда её координаты:
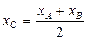 ,
, 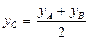 ,
, 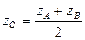 .
.
Дата добавления: 2022-02-05; просмотров: 459;











