Метод минимизирующих карт Карно (Вейча)
При минимизации логической функции от небольшого числа переменных удобным является графический метод представления функции с помощью диаграмм (карт) Вейча и их разновидности - Карно. Карта Вейча представляет собой развертку n-мерного куба на плоскости. При этом вершины куба представляются клетками карты, каждой из которых поставлена в соответствие конститутиента единицы или нуля. Переменные, обозначающие клетки диаграммы, расставляются таким образом, чтобы наборы, записанные в двух смежных клетках, имели кодовое расстояние, равное единице. Поскольку такие наборы располагаются в смежных клетках, они получили название соседних наборов. В клетку карты, соответствующую конституенте единицы, заносится 1, иначе − 0. Таким образом, для минимизации функции она должна быть представлена в форме СДНФ. Минимизация булевой функции с использованием карт в дизъюнктивной (конъюнктивной) форме заключается в объединении единичных (нулевых) клеток в контуры, каждому такому контуру соответствует простая импликанта.
Можно сформулировать следующие правила минимизации:
§ количество клеток карты в одном контуре должно быть равно 2n;
§ для контура, содержащего 2n клеток, должно быть n осей симметрии;
§ количество контуров должно быть минимально;
§ число единиц в контуре должно быть максимально;
§ контуры могут пересекаться, то есть некоторая клетка может входить в несколько контуров.
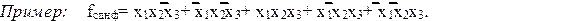
 
| х2 | |||
  x1 x1
|    1 1
|  1 1
|  1 1
| |
  1 1
|  Контуры
1 2 3 4 Контуры
1 2 3 4
| |||
| х3 |
| Рис. 15. Карта Вейча для fСДНФ |
На рис. 15 показана заполненная карта Вейча, соответствующая функции fСДНФ. На карте обозначены четыре контура, каждый из которых содержит по две клетки. Контур 2 можно считать лишним, так как он покрывает клетки, уже покрытые двумя другими контурами (1 и 3). Аналогично можно считать лишним контур 3 (покрывается контурами 2 и 4). Здесь возможны несколько тупиковых форм ФАЛ. Таким образом, по данной карте может быть получена одна из тупиковых форм:
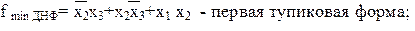
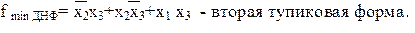
Если функция задана в форме ДНФ, то необязательно ее приводить к форме СДНФ, что является одним из преимуществ карты Вейча. Для этого рассматривается каждый дизъюнктивный член функции в отдельности, и в соответствующие ему клетки карты заносятся единицы.

| x2 | ||||
   
  x1 x1
| x4 | ||||

| x3 |
Рассмотрим сказанное на примере функции






 fДНФ=x1x2+ x1x2x3+ x1x2x3x4+ x1x2x3x4.
fДНФ=x1x2+ x1x2x3+ x1x2x3x4+ x1x2x3x4.
Первому члену ДНФ поставлены в соответствие четыре клетки карты, второму – две клетки, третьему и четвертому − по одной клетке соответственно (рис.16). Далее объединение единиц в контуры и выбор их минимального числа осуществляются рассмотренным выше методом.
| Рис. 16. Карта Вейча для fДНФ |
 
|
x2 | ||||
 x1
x1
|  0 0
| x4 | |||

| x3 |
| Рис.17. Карта Вейча для fкнф |
Если выбраны самые большие контуры и использовано по возможности меньшее их число, то будет получена самая простая дизъюнктивная нормальная форма. Дальнейшее упрощение можно получить за счет выполнения скобочных преобразований. Выражению с меньшим числом вхождений букв соответствует схема, имеющая меньшее число входов элементов, так что упрощение функций ведет к упрощению реализующих их схем.
 01 01
| ||||
Принимая во внимание клетки карт, не содержащие единиц, и поступая с ними так же, как мы поступали с клетками, содержащими единицы, можно получать конъюнктивные нормальные формы (рис. 17).
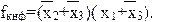
| Рис.18. Структура карты Карно |
Если логическая функция задана таблицей истинности, то более удобной для графического представления функции является карта Карно. В отличие от карты Вейча в карте Карно строки и столбцы закодированы r-разрядным кодом Грея. Код Грея – двоичный код, в котором рядом стоящие коды – соседние (их кодовое расстояние равно единице). В карте Карно каждой клетке соответствует код, состоящий из кода строки и кода столбца (рис. 18).
На рис. 19 показано соответствие клеток карты Карно и строк таблицы истинности. При этом в карте рис. 19,б показаны координаты единичных и нулевых значений функции, а в карте рис. 19,в показано соответствие строк таблицы истинности и ячеек карты.
| x1 | x2 | x3 | f | |

|
| б в Рис. 19. Таблица истинности и карта Карно |

| ||||
| 1 | 1 | |||
| 1 | 1 |
а
Дата добавления: 2022-02-05; просмотров: 759;












