Метод Блейка - Порецкого

Метод позволяет получать сокращенную ДНФ булевой функции f из ее произвольной ДНФ. Базируется на применении формулы обобщенного склеивания:

,

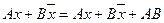справедливость которой легко доказать. Действительно,

, .

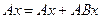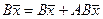Следовательно,

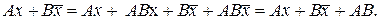
В основу метода положено следующее утверждение: если в произвольной ДНФ булевой функции f произвести все возможные oбобщенные склеивания, а затем выполнить все поглощения, то в результате получится сокращенная ДНФ функции f.

Рассмотрим пример. Пусть булева функция f задана произвольной ДНФ.

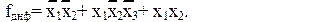
Необходимо, используя метод Блейка – Порецкого, получить сокращенную ДНФ функции f. Проводим обобщенные склеивания. Легко видеть, что первый и второй элемент исходной ДНФ допускают обобщенное склеивание по переменной х₁. В результате склеивания получим:

Первый и третий элемент исходной ДНФ допускают обобщенное склеивание как по переменной х₁, так и по х₂. После склеивания по x₁ имеем:

После склеивания по x₂ имеем:

Второй и третий элемент ДНФ допускают обобщенное склеивание по переменной х₂. После склеивания получаем:

Выполнив последнее обобщенное склеивание, приходим к ДНФ:

После выполнения поглощений получаем:

Попытки дальнейшего применения операции обобщенного склеивания и поглощения не дают результата. Следовательно, получена сокращенная ДНФ функции f. Далее задача поиска минимальной ДНФ решается с помощью импликантной матрицы точно так же, как в методе Квайна.