Статические характеристики и параметры измерительных устройств
В общем случае состояние (режим работы) измерительного устройства, при котором значения входного Х и выходного Y сигналов не изменяются, называют статическими (стационарными или равновесными).
Статической характеристикой измерительного устройства называют функциональную зависимость выходного сигнала от входного в статическом режиме работы указанного устройства. Более точно статическую характеристику можно определить как зависимость информативного параметра выходного сигнала от информативного параметра его входного сигнала в статическом режиме. Статическая характеристика описывается в общем случае некоторым нелинейным уравнением (уравнением преобразования):
| Y=ƒ(X) | (1.1) |
Для измерительных преобразователей, а также измерительных приборов с неименованной шкалой или шкалой, отградуированной в единицах, отличных от измеряемой величины, статическую характеристику принято называть функцией преобразования. Для измерительных приборов иногда статическую характеристику называют характеристикой шкалы.
Определение статической характеристики связано с выполнением градуировки, поэтому для всех средств измерений используют понятие градуировочной характеристики, под которым понимают зависимость между значениями величин на выходе в ходе средства измерений, составленную в виде таблицы, графика или формулы.
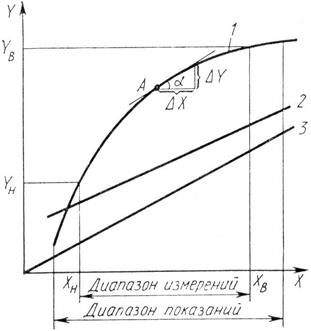
Рис. 1.4. Статическая характеристика измерительного устройства
На рис. 1.4 показаны виды статических характеристик измерительных устройств. За исключением специальных случаев, основное требование, предъявляемое к статической характеристике измерительных устройств, сводится к получению линейной зависимости между выходной и входной величинами. На практике это требование реализуется в общем случае только с некоторой принятой заранее погрешностью.
Кроме статической характеристики для определения метрологических свойств измерительных устройств используется ряд параметров.
На рис. 1.4 на статической характеристике 1 графически представлены упомянутые понятия диапазона показаний, диапазона измерений, диапазона измерений нижнего Хн и Yн и верхнего Хв и Yв пределов измерений (см. также рис. 1.3).
Диапазон показаний – область значений шкалы, ограниченная конечным и начальным значениями шкалы.
Диапазон измерений (рабочая часть шкалы) – область значений измеряемой величины (на шкале прибора), для которой нормированы допускаемые погрешности средств измерений (см параграф 1.6).
В частном случае указанные диапазоны могут совпадать.
Примечательно к измерительным устройствам вообще диапазон измерений часто называют рабочим диапазоном преобразований – наибольшее значение диапазона измерений. Нижний предел измерений – наименьшее значение диапазона измерений.
Из сказанного следует, что диапазон измерений определяется разностью значений верхнего и нижнего пределов измерений (Xв–Xн; Yв–Yн). Для количественной оценки влияния на выходной сигнал измерительного устройства входного сигнала в произвольной точке (рис. 1.4) статической характеристики служит предел отношения приращения ΔY выходного сигнала к приращению ΔХ входного сигнала, когда последнее стремится к нулю, т. д. произвольная выбранной точке
 . .
| (1.2) |
Применительно к измерительным приборам этот параметр называют чувствительностью и определяют как отношение измерения сигнала на выходе измерительного прибора к вызывающему его изменению измеряемой величины. Графически она определяется тангенсом угла наклона 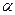 касательной (рис. 1.4), приведенной к выбранной точке A статической характеристики.
касательной (рис. 1.4), приведенной к выбранной точке A статической характеристики.
Если статическая характеристика измерительного прибора нелинейна (кривая 1 на рис. 1.4), то его чувствительность будет различной в разных точках характеристики, а шкала прибора – неравномерной. Приборы с линейной (прямая 2 на рис. 1.4) или пропорциональной (прямая 3 на рис. 1.4) статической характеристикой имеет неизменную в любой точке шкалы чувствительность и равномерную шкалу.
У измерительных преобразователей статическая характеристика, как правило, является линейной:
| Y=KX. | (1.3) |
Здесь К – коэффициент преобразования (или при использовании преобразователя в системах автоматического регулирования – коэффициент передачи), определяемы как отношение сигнала на выходе измерительного преобразователя, отражающего измеряемую величину, к вызывающему его сигналу на выходе преобразователя.
Для измерительных приборов важным параметром является цена деления, определяемая как разность значения величин, соответствующих двум соседним отметкам шкалы. Физически цена деления определяется количеством единиц входной величины, содержащихся в одном делении шкалы измерительного прибора.
Цена деления однозначно связана с числом делений n шкалы измерительного прибора. Последнее в свою очередь связано с погрешностью измерительного прибора, обычно представляемой его классом точности 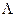 (см параграф 1.6). Число делений шкалы измерительного прибора, как правило, в первом приближении определяется из соотношения
(см параграф 1.6). Число делений шкалы измерительного прибора, как правило, в первом приближении определяется из соотношения
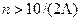 . .
| (1.4) |
При выполнении условия (1.4) число делений шкалы выбирают таким, чтобы цена деления составляла целое число единиц измеряемой величины.
В научно-технической литературе используется понятие порога чувствительности (порога реагирования) измерительного устройства, под которым понимают то наименьшее изменение входного сигнала, которое вызывает уверенно фиксируемое изменение выходного сигнала.
Как правило, наблюдатель, осуществляющий измерение, уверенно может заметить смещение стрелки на половину деления шкалы, поэтому порог чувствительности можно считать равным половине цены деления, а если учесть при этом соотношение (1.4), то в первом приближении порог чувствительности равен классу точности Λ.
Одним из важнейших условий получения корректных результатов измерений является учет взаимодействия измерительных устройств между собой и с объектом измерений.
При подключении измерительного устройства или преобразователя к объекту измерений последний потребляет некоторую энергию или мощность от объекта. Аналогичная ситуация имеет место при подключении измерительного прибора или преобразователя к выходу предыдущего по цепи измерения преобразователя. Это определяет необходимость учитывать свойства измерительных устройств отбирать или отдавать энергию через свои входные или выходные цепи.
В качестве характеристики указанного свойства принято использовать для измерительных устройств понятие входного импеданса (полного или кажущегося сопротивления), а для измерительных преобразователей – понятия входного и выходного импедансов. В общем случае под импедансом Z понимают отношение обобщенной силы N к обусловленной ею обобщенной скорости W:
| Z=N/W. | (1.5) |
В настоящее время понятие входного и выходного импедансов широко используется для электрических измерительных устройств. При этом импеданс определяется как отношение напряжения к току. Применительно к измерительным устройствам для неэлектрических величин в каждом отдельном случае требуется проведение исследований для установления наиболее целесообразной формы представления входного и выходного импедансов.
Погрешности измерительных устройств
Инструментальная погрешность (или погрешность измерительных устройств) имеет определяющее значение для наиболее распространенных технических измерений.
На рис. 1.6 приведена классификация погрешностей измерительных устройств по ряду признаков.
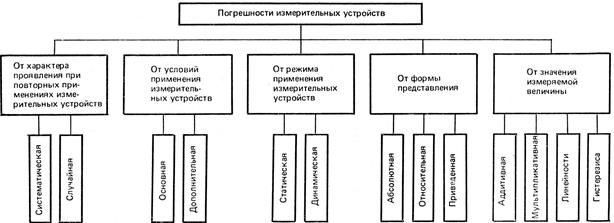
Рис. 1.6. Классификация погрешностей измерительных устройств
По характеру проявления при повторных измерениях одного и того же значения физической величины принято выделять систематическую и случайную погрешности (или составляющие погрешности) измерительных устройств. В эти понятия в основном вкладывается тот же смысл, что и в понятия систематической и случайной погрешности измерений <…>. Особенность здесь состоит в том, что всякое измерительное устройство предназначается для внесения определенности в исследуемый процесс, а наличие случайной составляющей погрешности приводит к неоднозначности. В связи с этим первая задача, которая обычно решается при создании измерительных устройств, состоит в том, чтобы случайную погрешность сделать незначительной. Если это условие выполняется, а элементы, входящие в состав измерительного устройства, стабильны, можно путем градуировки <…> обеспечить достаточно малые систематические погрешности измерительного устройства. Рассмотренная концепция используется как основная при создании рабочих средств измерений и, в частности, измерительных устройств для технологических измерений.
В зависимости от условий применения измерительных устройств различают основную и дополнительную погрешности (см. рис. 1.6).
Основной погрешностью средства измерений называют погрешность при использовании его в нормальных условиях. Нормальными условиями применения средств измерений называют условия, при которых влияющие величины имеют номинальные значения или находятся в пределах нормальной области значений. Нормальные условия применения указываются в стандартах или технических условиях на средства измерений. При использовании средств измерений в нормальных условиях считают, что влияющие на них величины практически никак не изменяют их характеристики.
Дополнительной погрешностью измерительного преобразователя (или изменением показаний измерительного прибора) называют изменение его погрешности, вызванной отклонением одной из влияющих величин от ее нормативного значения или выходом ее за пределы нормальной области значений. Дополнительная погрешность может быть вызвана изменением сразу нескольких влияющих величин.
Изменение погрешности, как и других характеристик и параметров измерительных устройств под действием влияющих величин, описывается функциями влияния <…>.
Иными словами, дополнительная погрешность – это часть погрешности, которая добавляется (имеется в виду алгебраическое сложение) к основной в случаях, когда измерительное устройство применяется в рабочих условиях. Рабочие условия обычно таковы, что изменения значений влияющих величин на них существенно больше, чем для нормальных условий, т. д. область рабочих (часть этой области называют расширенной областью) условий включает в себя область нормальных условий.
В некоторых случаях основная погрешность измерительных устройств определяется для рабочей области изменения значений влияющих величин. В этих случаях понятие дополнительной погрешности теряет смысл.
В зависимости от режима применения различают статическую и динамическуюпогрешности измерительных устройств.
По форме представления принято различать абсолютную, относительную и приведенную погрешности измерительных устройств (рис. 1.6). Для измерительных приборов и преобразователей определение этих погрешностей специфично. У измерительных приборов имеется шкала, отградуированная в единицах входной величины, либо шкала, отградуированная в условных единицах с известным множителем шкалы, поэтому результат измерения представляется в единицах входной величины. Это обусловливает простоту определения погрешности измерительных приборов.
Абсолютной погрешностью измерительного прибора Δ называют разность показаний прибора Хп и истинного (действительного) Хд значения измеряемой величины:
| Δ=Xп–Xд. | (1.11) |
Действительное значение определяется с помощью образцового прибора или воспроизводится мерой.
Относительной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к действительному значению измеряемой величины. Относительную погрешность выражают в процентах:
| δ=Δ100/Xд. | (1.12) |
Так как Δ<<Xд или Хп то в выражении (1.12) вместо значения Хд может быть использовано значение Хп.
Приведенной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к нормирующему значению ХN. Приведенную погрешность также выражают в процентах:
| γ=Δ100/XN. | (1.13) |
В качестве нормирующего значения используется верхний предел измерений, диапазон измерений и др., т. е.
| γ=Δ100/(Xв–Xн). | (1.14) |


Рис. 1.7. Реальные функции преобразования измерительных устройств
Аддитивной (получаемой путем сложения), или погрешностью нуля измерительных устройств, называют погрешность, которая остается постоянной при всех значениях измеряемой величины.
На рис. 1.7, а показано, что реальная функция преобразования Y=ƒр(X) несколько смещена относительно номинальной Y=ƒн(X) т. е. выходной сигнал измерительного устройства при всех значениях измеряемой величины X будет больше (или меньше) на одну и ту же величину, чем он должен быть, в соответствии с номинальной функцией преобразования.
Мультипликативной(получаемой путем умножения), или погрешностью чувствительности измерительных устройств, называют погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины.
Графически появление мультипликативной погрешности интерпретируется поворотом реальной функции преобразования относительно номинальной (рис. 1.7, в).
Дата добавления: 2018-05-25; просмотров: 2857;











